Compiler Design `CMPUT415`

V00 - Lexical Analysis and Parsing

Lexical Error: A token not in the vocabulary (lexicon) is not in the phrase Parsing error/Syntax error: the phrase is not part of the valid language that is recognized by the grammar Semantic error: The input is grammatically correct but semantically meaningless

Aside: this implies that one could create a "semantic grammar" that only recognizes semantically meaningful phrases; clearly this would be much more fuzzy in natural language
Aside: this is linked to compile time (static) vs. runtime (semantic?) errors

Overview of Language Processing

The input is in the form of a stream of characters. The lexer/tokenizer groups this stream of characters into a stream of tokens, which are the atomic units of the language. Next, a parser builds the token stream into a parse tree by matching patterns of tokens to parser rules in the grammar, which describes how tokens form sentences.

Note that tokens are terminal nodes in the grammar (i.e. leaf nodes of the parse tree), whereas rules are defined in terms of other nodes in the tree (i.e. are interior nodes).
Tokens are described by lexer rules

The parse tree may be further refined (e.g. into an AST), then used for something semantically meaningful. An interpreter would traverse this tree and evaluate the computation following the structure of the tree itself. A compiler would translate the tree into another program in a lower-level language.

Note that ancillary data structures (e.g. symbol table, flow graph, scope tree, etc.) may be required to properly evaluate/compile the program.

Grammar Example: Generator Parser

Regular expressions are particularly useful for parsing, since they perform the same task that the parser does, just one level down; regex deals with individual characters. As such, they are particularly useful for matching tokens.

grammar Generator;

// a file is a bunch of statements
file: stmt* EOF;

// operator precendence is encoded in these rules
expr: '(' expr ')'                            #parenExpr 
    | <assoc=right> expr op=EXP expr          #expExpr
    | expr (op=MUL | op=DIV | op=MOD) expr    #mulDivModExpr
    | expr (op=ADD | op=SUB) expr             #addSubExpr
    | INT                                     #intExpr 
    | ID                                      #idExpr
    ;

stmt: '[' ID IN INT '..' INT '|' expr']' ';';

// TOKENS

// reserved words
// these should be at the top so they match before other stuff
IN: 'in' ;

// integers
INT: [0-9]+ ;
// identifiers
ID: [a-zA-Z][a-zA-Z0-9]* ;

// operator tokens
ADD: '+';
SUB: '-';
MUL: '*';
DIV: '/';
MOD: '%';
EXP: '^';

// to skip
WS: [ \t\r\n]+ -> skip; 
LINE_COMMENT: '//' .*? ('\n' | EOF) -> skip;

A few notes

By convention, tokens are declared in upper case and parse rules in lower case. ANTLR is opinionated towards this convention; it enforces it on you.
ANTLR grammars are left-associative by default; we can use the <assoc=right> tag to force the grammar to parse from the right
We can set op= tags for particular entries in grammar rules to "group" them together; this makes them easier to manage later.
We can use #tags to abstract out the parsing of each rule case (with |) into its own handler in the backend
-> skip tells ANTLR to skip over whatever matches the rule; this is often used for whitespace, comments, etc.

Regular expressions reference: https://docs.workato.com/regex.html

V01 - Building an (LL1) Lexer and Parser from Scratch

Lexer from Scratch

We define a function getNextToken() that grabs the next token from the input stream. Then, we have a main conditional with an entry corresponding to each type of token; the expression in the if-statement more or less matches the regular expression to match the first character.

Inside each conditional body, we know which type of token we are trying to recognize. So, we continue fetching tokens from the input stream (in another while loop) until we fail to match the rule that recognizes characters in the token. At this point, we return the token (or, alternatively, the index that it ends at).

For single character tokens, we simply check if the character is equal to each token. We can use a switch statement for this because the order of conditionals will not matter.

The lexer simply calls getNextToken() until there are no tokens left.

Philosophy of the Lexer

The lexer matches the longest expression that it can; it only stops matching when it finds a character that cannot be in the token. It's then that it returns.

The lexer is also do or die; once it matches to a specific type of token, it fetches from the input stream until it matches the token completely as described above. So, if it matches something we don't want it to, it will keep burning the input stream; those characters will be gone forever.

We must keep this in mind when describing languages with grammars; we are making a tradeoff where the rules we can write are more constrained in structure, but the resultant lexing process is elegant and efficient.

Finally, the order of the conditionals matters; the lexer will try to match to rules in order, so if a character can match to multiple tokens, the lexer will pick the first one. So, the order of rules in the grammar does make a difference if there exist characters that could be the first character of multiple tokens.

Code

In this example, we parse words and numbers.

// enum with ID and INT

Token getNextToken() {
    // skip whitespace
    do { c = getchar(); } while (c == ' ' || c == '\n'); 
    
    // if starting to lex a word
    // [a-zA-Z]
    if('a' <= c <= 'z' || 'A' <= c <= 'Z') {
        // lex the rest of the word
        // [a-zA-Z]*
        do { c = getchar(); } while ('a' <= c <= 'z' || 'A' <= c <= 'Z');
        // return whatever (we would keep track of it before)
        return ID;
    }
    
    // if starting to lex a number
    // [0-9]
    if('0' <= c <= '9') {
        // [0-9]*
        // lex the rest of the number
        do { c = getchar(); } while ('0' <= c <= '9');
        // return whatever (we would keep track of it before)
        return INT;
    }
}

Parser from Scratch

We are given a stream of tokens. Like the lexer, we check the value of the first token, pick the corresponding rule, then read the token stream until we match a complete rule.

It is useful to define a match(TOKEN) function that fetches the next token from the stream and makes sure that it is of the correct type.

We also define a function for each type of rule that parses it. This "rule function" can recursively call other "rule function"s.

Finally, this example has a lookahead. This peeks at the next token in the stream. Sometimes, this is needed to figure out which case we need, e.g. if we have a recursive expr that can be expr + expr, expr - expr, etc.

If our parser looks ahead at most $n$ tokens, it is a LL(n) parser. If there is no limit, it is an LL* parser; this is what ANTLR is.

Code

// recognize a statement
void statement() {
    // there are multiple types of statements
    // so the statement function just delegates to these
    // it's a "RULE -> RULE" rule, kinda like syntactic sugar
    switch(cur_token) {
        case ID:
            assign_stmt();
            break;
        case IF:
            if_stmt();
            break;
        case WHILE;
            while_stmt();
            break;
        // ...
    }
}

void assign_stmt() {
    // assign_stmt: ID = expr ;
    // this is an "and"/"product" in the sense that there's an
    // ID and a EQUALS and an expr and a semicolon
    // so, the matching happens in succession instead of as an if/switch
    // further cements the orifsum and andthenprod 
    match(ID);
    match(EQUAL);
    expr();
    match(SC);
}

// ????????? seems iffy
void expr() {
    match(INT);
    // foreshadowing
    if(!lookahead('+')) {
        return;
    }
    match('+');
    expr();
}

this code looks iffy

V02 - Language Hierarchy

Grammars generate languages, which can be recognized Languages, in all forms, follow a tree structure

Automata Theory Terms

In increasing order of generality:

Combinational Logic < Finite-state machines < Pushdown Automaton < Linear-Bounded Automaton < Turing Machine

Combinational logic: circuits whose output depends only inputs; these can be described by logical expressions
Linear-bounded automaton: only a specific piece of the tape can be accessed by the automaton

define all of these

Language Hierarchy

Again, in increase order of generality:

A regular grammar is, broadly, a grammar works like a regular expression. They have no memory of what was generated in the past, and as such can be implemented with a state machine (which is how regular expressions are implemented).

It must be left-linear or right-linear, i.e. the only non-terminal node in a rule has to always be on the left or on the right

A context-free grammar has no context constraints; it can generate a language without additional context, i.e. knowledge about what has already been seen and what structure the recognizer is "in". It can be implemented with a pushdown automaton.

Generally, any combination of terminals and non-terminals is context-free; there can be multiple non-terminals in a rule, at any space. However, we still have to be careful of ambiguity
The non-terminals can be expanded in any order without changing the result
E.g. a context-free grammar can describe a palindrome, but a regular expression can't

A context-sensitive grammar needs context to generate a language. We can think of this adding "states" to a parser; the parser may choose to match to different expressions based on the state, and the state can be changed by recognizing a rule. They can be implemented with linear-bounded automata.

So, a rule may look like "in context $A$, replace pattern $x$ with pattern $y$. In context $B$, replace $x$ with $z$, etc.". Rules are now $(\text{State}, \text{Pattern}) \to (\text{State}, \text{Pattern})$.
Aside: this is related to the notation of pure functional vs. imperative languages and side effects.

A recursively-enumerable grammar/language can only be recognized by a Turing machine. If a given input is in the language, it will be accepted by the Turing machine. Otherwise, the input is rejected, or the machine loops forever.

CSGs with ANTLR

ANTLR lets you define context-sensitive grammars with -> pushMode(my_state), which we can use to push a new state onto a context stack. Then, we can define rules under a mode my_state: statement to bind them to the particular state.

Aside: it seems like -> broadly means that the evaluating the rule produces a side-effect.

Extra reading: Formal language theory: refining the Chomsky hierarchy.

V03 - Ambiguity

Kids make bad hamburgers

Ambiguity

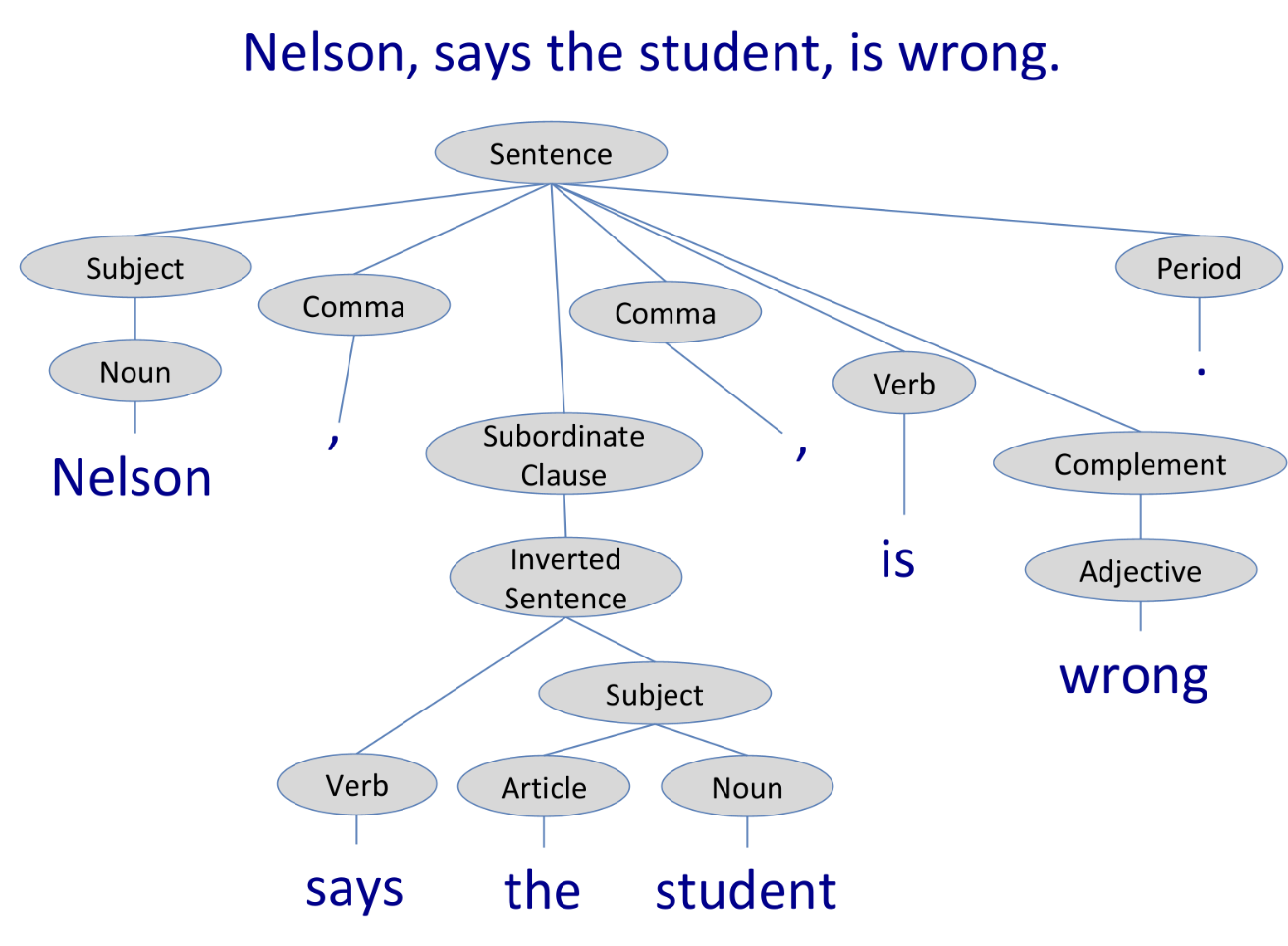
A sentence is ambiguous if it can be validly parsed into more than one semantically different trees.

E.g. in English, the word "kids" in "kids make bad hamburgers" can be understood as either the subject or object (?) of the sentence; these interpretations have (very) different meanings
E.g. in C, i * j could mean the expression "i times j", or "j is a pointer of type i"; this comes from the fact that * has multiple different meanings.

A language is ambiguous if it contains at least one ambiguous sentence, i.e. a grammar is ambiguous if it contains a sentence that can be built into two distinct parse trees.

WWAD: What Would ANTLR Do?

As mentioned previously, ANTLR will try to match rules in order. Thus, if a grammar is ambiguous, ANTLR will pick the interpretation that is listed first.

ANTLR never backtracks

Ambiguity forces the lexer to pick between principles: match the longest possible string, or traverse the language without backtracking? This is a design decision; ANTLR chose the latter option.

check correctness?

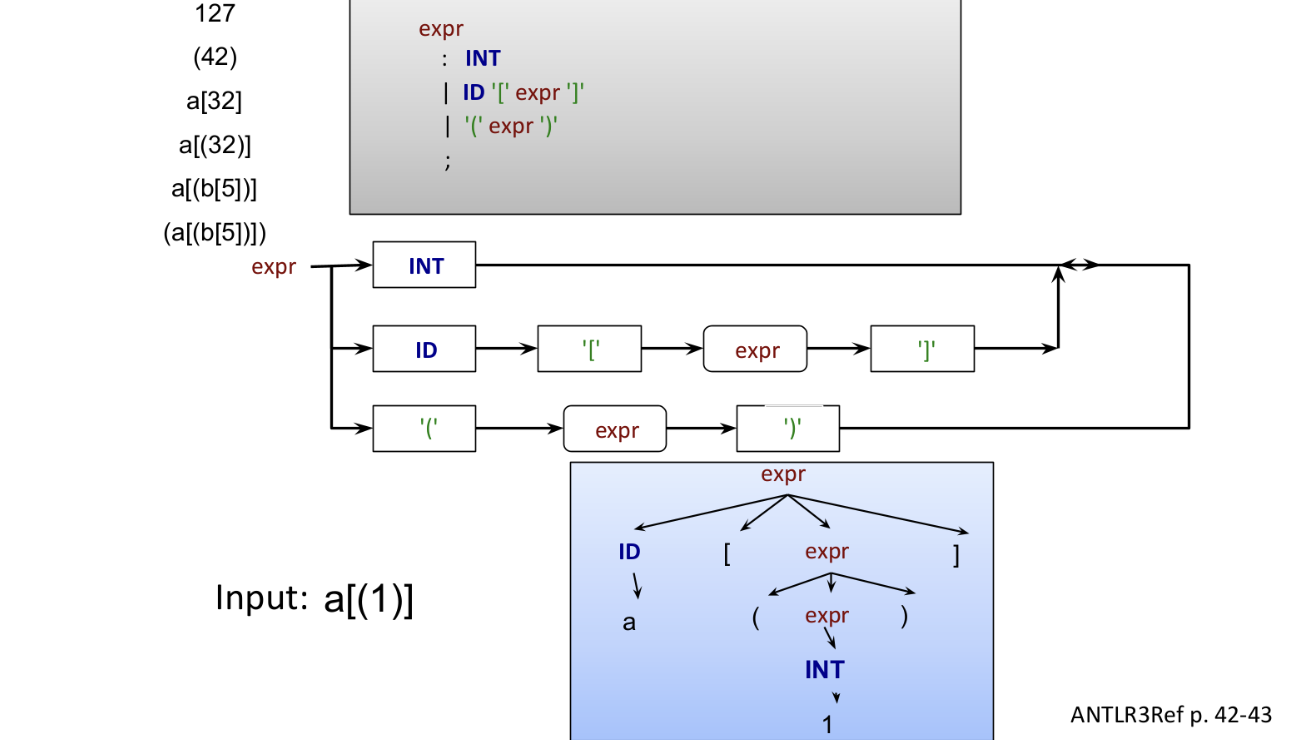
Different Ways to Illustrate a Grammar

V04 - LL and LR Recognizers

Both of these read input from left to right, but differ in how they attempt to match the input.

LL Parsers

An LL parser explores the leftmost derivation of the rule it is examining. In that sense, it is top-down: it starts with a rule (namely, the first one) in mind and tries to match to other rules as it goes. So, it is goal-oriented.

LL parsers are characterized by traversing the tree via depth-first search.
Aside: this "goal-oriented" behavior is similar to the unification algorithm underlying prolog; is this the interpreter equivalent to an LL parser? How can we relate these two structures?

LL Parsers are also called descent parsers because they start at the top of the tree.

LR Parsers

In contrast, an LR parser will consume tokens until it finds a complete sentence that it can match the accumulated tokens to, i.e. it builds the parse tree from the bottom up. It must find the rightmost character before it can match to a rule; it takes the rightmost derivation.

correctness: LR Parsers more or less follow breadth-first search; it tries to match the entire program to a rule, then recursively matches the sub-rules implied by its choice

Characterizing Parsers

We can characterize parsers with the following attributes

Traversal strategy: descent | ascent, i.e. top-down vs. bottom-up
Recursion?: recursive | not recursive
Lookahead: $n\in \mathbb{N}\cup\set{\star}$: how many tokens do we need to look ahead to recognize the language?
- $\star$ denotes that any number of tokens can be used

ANTLR generates LL(*) recursive descent parsers by default. However, we can bend its output to our will, e.g. by declaring <assoc=right> before a rule to force ANTLR to parse it from the right (correctness).

V05 - Parser Generators

But what is ANTLR?

Left-Recursion

A left-recursive rule is a rule of the form $\text{r} \to \text{r} \, X$; the leftmost entry in the rule is a recursive call to that rule itself. This causes infinite loops in recursive descent parsers, since they descend the leftmost recursive expression first every time and never get to the "base case", if one exists.

E.g. a recursive descent parser generator may produce the following code

// RULE:
// r: r X

void r() {
    r();
    match(X);
}

// clearly, we never reach match(X)

Fixing the Problem

If operations involved in a rule are commutative, we can "switch" the order of the nodes; we write the non-recursive rule first. E.g. since $+$ is commutative on $\mathbb{Z}\times \mathbb{Z}$, the two expr definitions are equivalent:

// left-recursive
expr : expr "+" INT | INT;
// not left-recursive
expr : INT "+" expr | INT;

However, if we have some operation that isn't commutative (or worse, also isn't associative), fixing the problem is not as trivial. But even if it were, we usually want to do more than simply recognize a language; we want to parse, which requires more structure.

It figures that sometimes, describing a grammar with left-recursion makes sense. Thus, the parser must adapt.

ANTLR and Left Recursion

ANTLR 4 allows for direct left-recursion, i.e. it allows grammars like

expr
    : expr '+' expr
    | ...
    | INT;

This is done by rewriting recursive rules.

note: we were shown slides for this but they aren't in any of the notes online. I should request these

V06 - Building a Recursive-Descent Recognizer from a Grammar

Program Structure

We can translate concepts in the grammar to constructs into constructs in the OOP paradigm. The entire parser is encapsulated into a class, which holds everything that affects the current state of the parser i.e. current token, lookahead token(s), input stream, etc.

public class G extends Parser {
    // token INT type definitions
    // constructors as needed
    // methods for rules
}

Rules and Tokens

Each grammar rule $r$ becomes a method public void r() in the parser class

The entries of the rule become a begin-type sequence of corresponding function calls
Each token $T$ referenced in a rule becomes a match(T) call in the function of the rule that called it

Each token $T$ is mapped to a unique integer public static final int T

There are two special types of tokens: INVALID_TOKEN = 0 mapping to an invalid token, and EOF = -1 to denote the end of the file
Storing tokens as names of integers makes them easy to work with in Java
- Aside: this is a good trick to have in a back pocket for adding "symbols" to a language
- Aside: are LISP symbols implemented this way?

Matching

Since our parser is LL, we must try to match alternatives. This is done by iterating through all the possible matches (i.e. that layer of the tree), looking at the current token (and possibly lookahead), and matching to the first correct option.

If we don't match to something after the options have been exhausted, we throw a hissy fit (i.e. an exception)
As a point of software engineering, we can abstract the "does this token predict this rule" computation into a function, and simply call that function on the token in the if-statement

Single-token lookahead can be implemented with a switch statement, since we can just switch based on the value of the lookahead token directly.

Regex Constructs

Optional (T?): we attempt to match as per usual, but if we don't match to anything, we don't throw an exception (or do anything).

One or more (T+): we use a do-while loop instead of an if-statement for that particular clause

Zero or more (T*): we use a while loop instead of an if-statement.

Aside: this illustrates the difference between while and do-while: do-while executes the code inside once, then starts checking the loop condition. While checks immediately.

Non-greedy Rules

A non-greedy rule is (roughly) a rule that can be stopped by something. E.g. LINE_COMMENT: '//' .* would consume everything in the file after the comment; we want it to stop when it sees \n. We can specify LINE_COMMENT: '//' .*? '\n' to do just that.

Under the hood, the regex engine (or our code) will keep matching everything to .*, but it will check each time if the current token instantiating . is \n. If so, it will match the '\n' in the rule instead.
E.g. we can implement a non-line comment: '/*' .*? '*/'

V07 - Lookahead Sets and non-determinism

We define two types of lookahead sets:

FIRST defines which tokens can start a rule's alternative.
FOLLOW defines which tokens can come after the rule's alternative

Point of disambiguation: an alternative is an "or" clause in a rule; e.g. a stmt can be an if or a while or a for etc.

FIRST

The FIRST set for a given alternative is (generally?) the set of tokens needed to uniquely identify that particular alternative when the parser is looking at the rule it's part of.

E.g.

stmt
    : 'if'        // lookahead: { if }
    | 'while'     // lookahead: { while }
    | 'for'       // lookahead: { for }
    ;

body_element
    : stmt        // lookahead: { if, while, for }
    | LABEL ';'   // lookahead: { LABEL } (we don't need ';' since "LABEL" already gives us everything we need to know to know which alternative to pick)
    ;

FOLLOW and Empty Alternatives

The FOLLOW set defines which tokens (possible just terminals? check) that could possibly appear after an alternative in a rule. We need it when the FIRST set includes every node in the rule and still doesn't provide enough information.

Identity: For lookahead set $S$, $S\not\subseteq \text{FIRST}\implies S\cap\text{FOLLOW}\ne \emptyset$, i.e. if $S$ overfills the $\text{FIRST}$ set, it spills into the $\text{FOLLOW}$ set (correctness)

A rule may be an empty alternative, i.e. one of the alternatives to the rule is $\varepsilon$, which represents a "nothing" and ultimately gets translated into the empty string.

If a rule has an empty alternative, the FIRST set of that alternative is the FOLLOW set of the rule itself
So, to define and use this FIRST set, we need to find a FOLLOW set

To determine the follow set, we need to be aware of the rest of the grammar.

Non-determinism

A parser is non-deterministic over a particular rule in a grammar if the lookahead tokens do not uniquely determine the rule's alternatives.

E.g. An LL(1) parser is non-deterministic on expr : ID '++' | ID '--'; because it can only look ahead by one token, and thus can only see ID. In contrast, an LL(2) parser is not non-deterministic over expr because it can look ahead far enough to distinguish the alternatives using '++' and '--'.

In this case, we say expr is LL(2).

Left-factoring

We can left-factor a rule by consolidating different cases with the same prefix into a single logically equivalent case with that prefix and a grouped set of alternatives:

expr : ID '++' | ID '--'; 
// vs.
expr : ID ('++'|'--');

This reduces non-determinism by reducing the number of rules; the delegation into "alternatives" is deferred to the next recursive level, i.e. when the members of the rule are matched.

Aside: this seems to cross over into the domain of logic; it reminds me of putting things in normal form. It also reminds me of unification as well.

Some left factoring rewrite rules

r : A B | A C  -->  r : A (B|C)

r : A | A B  --> r : A (B)?

Aside: We can define $?$ as a function of $\varepsilon$: $B? \equiv (B|\varepsilon)$

V08 - LL(k) Recursive-Descent Parser Example

We build an LL(k) Recursive-Descent Parser in Java; its goal is to parse nested lists in the form [a, b, [c, d], e …]

Java my beloved 🤮
Aside: making a parser generator would be a cool side project.

Program Structure

Parser Class

public abstract class Parser() {
    Lexer input;
    Token[] lookahead;
    int k;      // lookahead symbol count, i.e. size of buffer
    int p = 0;  // next position to fill in circular buffer
    
    public Parser(Lexer input, int k) {
        this.input = input; this.k = k;
        // create lookahead buffer
        lookahead = new Token[k];
        // fill up the circular buffer
        for (int i = 1; i <= k; i++) consume();
    }
    
    public void consume() {
        lookahead[p] = input.nextToken();
        // get the next circular buffer address with mod operator
        p = (p+1) % k;
    }
    
    // fetch next token from circular buffer
    // LT: load token
    public Token LT(int i) {
        return lookahead[(p+i-1) % k]
    }
    
    // get type of next token (needed for matching non-literal tokens)
    public int LA(int i) {
        return LT(i).type;
    }
    
    // match function
    public void match(int x) {
        if(LA(1) == x) consume();
        else throw error("Expecting " + input.getTokenName(x) + "; found " + LT(1));
    }
}

Lookahead Parser Class

This extends the parser by adding methods for the specific grammar rules.

public class LookaheadParser extends Parser {
    pubic LookaheadParser(Lexer input, int k) {
        super(input, k);
    }

    // match to '[' elements ']'
    public void list() {
        match(LookaheadLexer.L_BRACKET);
        elements();
        match(LookaheadLexer.R_BRACKET);
    }
    
    // match to INT, ..., INT
    void elements() {
        element();
        while(LA(1) == LookaheadLexer.COMMA) {
            match(LookaheadLexer.COMMA);
            element();
        }
    }
    
    // etc
}

Driver

Just in case you forgot how "public static void main string args" works

public class Test {
    public static void main(String[] args) {
        ListLexer lexer = new ListLexer(args[0]);
        ListParser parser = new ListParser(lexer);
        // begin parsing at the "top level" rule
        parser.list(); 
    }
}

Buffering the Token Stream

LL(k) parsers need lookahead. Sometimes, a lot of lookahead. We must buffer the token stream in order to handle this lookahead efficiently.

Note that the token stream is theoretically infinite; our data structure must handle this somehow (aside: there's probably an algebraic connection here about finite structures)

We can use a circular buffer for this task. Each time we read the next token, the previous one is replaced with the newest token that isn't in the buffer already. Thus, the input "snakes around" the buffer.

A buffer of size $N$ gives us $N$ characters of lookahead while loading exactly $N$ characters
Note: character $a$ is written at $\text{Buffer}[a \mod N]$; the cyclical behavior is inherited from the mod operator

Non-LL(k) Grammars

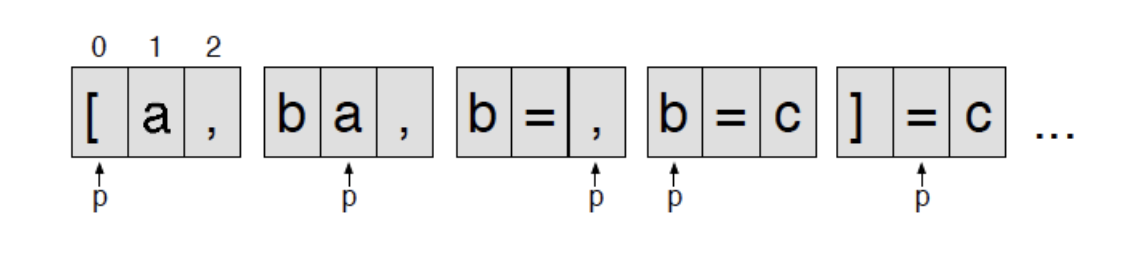
In some cases, a language cannot be parsed by an LL(k) parser, for some fixed $k\in \mathbb{N}$, namely the first rule of a grammar starts with a star pattern, and thus can match to any number of tokens/rules.

Appendix: Why Doesn't Our Program Do Anything?

Right now, the program doesn't really output anything; it just parses the input, i.e. makes sure it's valid according to the grammar. Later, we will see that we can include implementation language (here, Java) code in the grammar directly. It's this code that will get run as part of the rule methods and produce a meaningful result.

V09 - Listeners and Visitors

Discovery and Visit order

A search algorithm will discover nodes in its discovery order. E.g. DFS on the tree (+ (a) (b)) has discovery order + a + b +. Note how the discovery includes passing back through parent nodes.

E.g. algorithms: depth-first search (DFS), breadth-first search (BFS)

Relatedly, a traversal of a graph is the order in which its nodes are first visited. Trees, in particular, are amenable to certain traversals (wording, this sucks)

Preorder (top-down): visit the parent first, then the left and right child, i.e. + a b
In-order: visit the left child, then parent, then right child, i.e. a + b
Postorder (bottom-up): visit the left and right child, then the parent, i.e. a b +

We can see that traversals are characterized by the order of visiting the two children and parent, so there are $3!=6$ traversals of binary trees. However, the location of the parent is usually the most important; if we fix that the left child must come before right, we get the list above.

It's like normal vs. "cursed" trampoline skills: we define a usefulness heuristic that captures the traversals that usually get used

A mixed traversal may include preorder, in-order, and postorder actions; these are inserted before, between, and after the visitations of child nodes, respectively.

Aside: in my opinion these terms should be switched: discovery should happen only once, whereas visiting could happen more than once. Real Iceland/Greenland situation here. prankd.

Walking the Parse Tree

We visit the parse tree by defining a walk() function on each node. Generally, this function will perform something related to the function of the current node and call walk() on its children, if present.

The implementation of walk() defines how we traverse the tree.

Note that mixed traversal is useful for parse trees, e.g. parsing an AST into a LISP-style s-expression:

void walk() {
    // preorder actions go here
    // note: for LISP printing in particular, checking if we're not in a leaf
    // lets us avoid printing every integer literal, etc. in ()
    print("(");
    print(curNode.operator);
    left.walk();
    // in-order actions go here
    right.walk();
    // post-order actions go here
    print("(");
}

Listeners and Visitors

Motivation

Listeners and visitors are both patterns for traversing trees with data. In the context of parse trees, these patterns provide a way to implement the "next step", e.g. evaluating the program directly (an interpreter) or translating it into another language (a compiler).

These patterns create a layer of abstraction between the grammar and this "next step"; they decouple the grammar itself from the application code. Thus:

The grammar is easier to re-use, since we can just add another listener/visitor to it
- The grammar isn't bound to a particular "next level"; this would happen if we defined the output in the grammar directly, which is how things used to be done
Changing the grammar only means updating the methods relating to the changes, not the entire application code itself
Code is more modular → easier to isolate and debug problems
The application code is properly encapsulated

More on this software engineering later.

Visitor Pattern

A visitor pattern involves defining a visit() method for each type of node in the tree. The traversal is implicitly defined by the visit() function implementation; visit() should be called recursively on the children of the current node. The traversal is initiated by calling visit() on the root node of the parse tree.

Results are returned from child visitor methods to be used in the parent visitor method.

As such, visitor methods closely mirror the structure of an interpreter

Listener Pattern

A listener pattern involves defining an enterNodeType and exitNodeType method for each type of node in the tree. When a node is first visited, its corresponding enter function is called; when all its children have been visited and we are done with that node, we call its exit method.

So, we don't have any control of the order of visitation
Guarantees may be made about the visit order, e.g. ANTLR guarantees that the listener visits the tree in DFS order.

Generally, using a listener (and, even more generally, traversing with DFS) requires the use of a stack to handle things like expression parsing (more on this in V0C).

WWAD

We can use ANTLR to generate templates for visitors and listeners for a given grammar. Specifically, ANTLR generates a base listener/visitor class that defines all the visit/(exit, enter) functions. Your listener/visitor should inherit from the base and override these function definitions.

Refactoring guru: visitor pattern and listener/observer pattern

V0A - Decoupling Grammars from Application Code

We decouple the grammar from the application code by using the visitor and listener patterns, as covered in V09.

Embedded Actions

We can (ANTLR3?) embed actions in the grammar; this lets use do the "next step" directly in the grammar, as the input is being lexed and parsed. In ANTLR, we can add actions to the grammar with {} syntax.

This removes a pass through the input; everything gets done in one pass
However, the grammar and the application are tightly coupled → ugh

grammar exprs;

exprs = {
    // Java code here
    // start handling exprs (i.e. enterExprs)
    // note: we can access nodes in the rule with $ID if ID is in the rule, etc.
} expr+ {
    // Java code here
    // exitExprs
};

ID : [a-z]+;
//etc.

Beginning to Decouple

A preliminary way to decouple the grammar is to only call output-agnostic functions in the embedded Java code, e.g. handleExprs(), instead of embedding the code directly. This lets us handle multiple languages, i.e. we can have different (polymorphic) implementations of handleExprs() for an interpreter, compiler to C, compiler to RISC-V, etc.

Each backend you want to use is a subclass of the parser
But we're still tied to Java

Full Decoupling

As mentioned previously, we can generate a listener or visitor that does a completely separate walk over the parse tree. Then, to define a "next level", we inherit from the base visitor/listener and override-implement all the functions.

ANTLR also defines a maximally general ParseTreeListener class, which implements methods that work on any parse tree: visitTerminal, enterEveryRule, exitEveryRule, visitErrorNode.

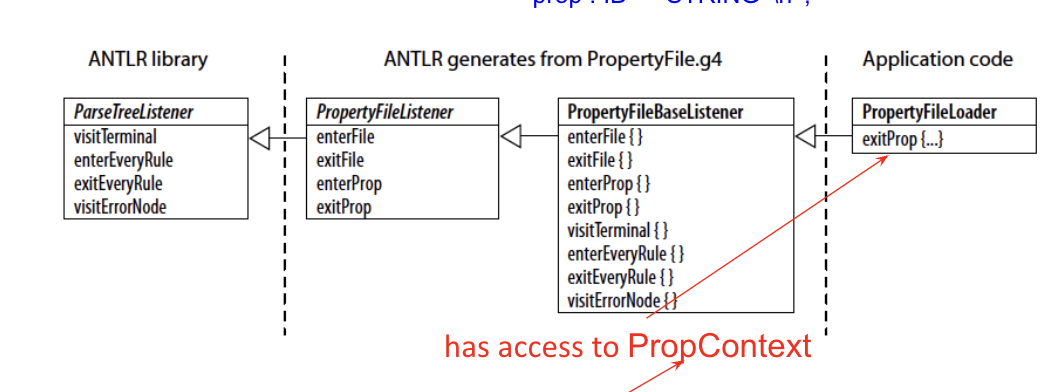
The full ANTLR class structure is as follows:

Code

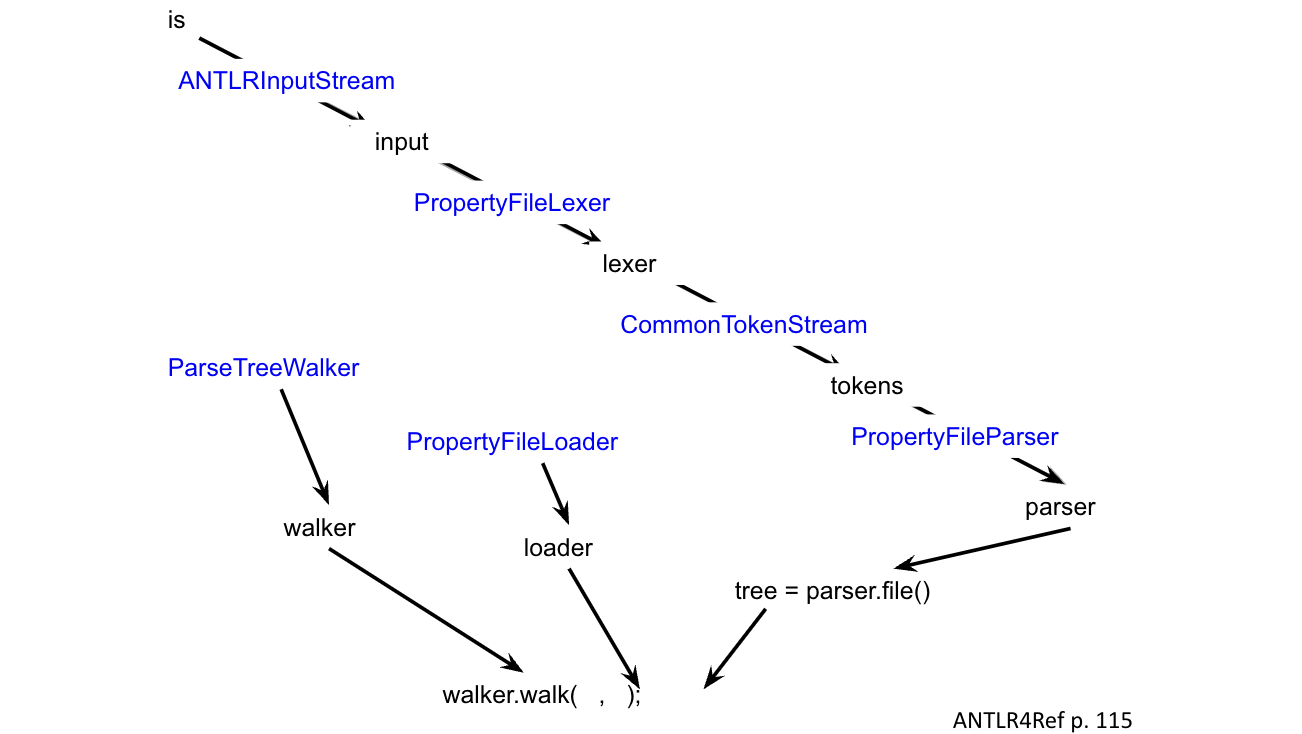
Code for all of this is in the V0A slides; might transcribe it here later.

V0B - Handling Alternatives Ergonomically

Say we have a large rule with lots of alternatives (expr being a canonical example). Each time we enter, exit, or visit an instance of that rule, we have to reach into the context (i.e. the ParseTreeContext ctx parameter in ANTLR-generated visitors/listeners) to figure out which alternative (here, which operator) we picked.

This is a pain in the ass and leads to messier code than is needed

In ANTLR, we can add labels to alternatives. This directs ANTLR to generate specific enter/exit/visit methods for each label, instead of for the rule in general.

As such, if we define a label for one alternative, we must define one for all of them
Aside: labels seem like directives that cause rules with many alternatives to be desugared into multiple rules with no alternatives. So we retain the elegance of defining them as alternatives in the grammar, but don't have to deal with the tiresome conditionals in the visitor/listener.

Example

We define the expr rule:

expr
    : expr op=MULT expr     #Multiplication
    | expr op=ADD expr      #Addition
    | //...                 #...
    | INT                   #IntegerExpr
    ;

With a visitor, this generates visitMultiplication, visitAddition, etc. methods instead of a single visitExpr method. Analogous methods are generated for a listener.

more code in the slides → transcribe later

event methods?? and why can't they pass information around?

does a regular visit/listen method still get generated, or just the alternatives?

In an event method, we might want to pass values down into the children or up into the parent. However, we can't define our own parameters because they change the signatures of the generated event methods. What do?

Disambiguation: an event method is a enter/exit/visit method corresponding to some rule in a grammar.

We have 3 main methods of sharing information among methods

Returning a value from a visitor method (i.e. a visitor must be used)
Create a shared field among event methods that everyone can read/write to
Add annotations to the parse tree to store needed values.

Returning Values from `visit`

We may simply return the value we need when we are done visiting a rule. E.g. visiting an expression that adds two integers returns the resulting integer.

This is elegant and space-efficient because storage of temporary results is kept to a minimum
However, we still can't define arguments (i.e. pass data parent → child) and each return value must of the same type*

(*) In ANTLR's generated C++ visitor methods have return type std::Any. Thus, we return a result of any type we want and use an any cast (std::any_cast<target_type>(visitor_result)) to retrieve that result in the parent.

However, this is clearly error-prone and hard to debug when it fails. A particular cast to boolean in SCalc comes to mind for me.

Stack Method

In the stack method for listener value passing, we simply keep a stack in the main object, which is accessible to all the event methods. When we enter a terminal value that we'll need, we push it to the stack. Then, when exiting the rule, we pop the arguments we need off the top of the stack, use them to product any return values we need, and push those to the stack.

This works particularly well for expression parsing, the stack utilizes reverse Polish notation.
The ability to use a stack to store arguments this way follows from the fact that the listener is guaranteed to use DFS to traverse the tree

This is also space efficient (since no data is attached to the tree), with the added advantage that multiple expressions can be passed and returned (!) with each event method. However, the implementor is responsible for managing the stack manually, which gives them enough rope to hang themself with.

Parse-Tree Annotation (Listener or Visitor)

Instead of storing intermediate data on The Stack, we can store it on the tree itself with annotations. Essentially, we walk through the tree and annotate a node with its corresponding intermediate value. Working through the tree bottom-up, we eventually arrive at the root note with the full result we need.

ANTLR doesn't generate the infrastructure needed to annotate directly on the tree, so we must create a map Values : ParseTreeNode -> Value to store and retrieve from.
When we get to a node in the tree, we check if it's in the map. If not, we add an entry with the node as a key and the value as a value. If it is, we simply retrieve the value from this map
This map has the type ParseTreeProperty<Integer>; ANTLR makes this type for us to enable use to use this method

class InterpreterWithProps extends ExprBaseListener {
    // node -> value map
    ParseTreeProperty<Integer> values = new ParseTreeProperty<Integer>();
    
    // ...
    // IN A METHOD
    // annotating a node
    values.put(cur_node, cur_value);
    // retrieving a value from a node
    values.get(cur_node)
}

Parse tree annotation lets us provide arbitrary information because any method in a listener or visitor can access the map whenever it wants, and thus can access information about other nodes in the tree.

Like the stack, we can also pass and return multiple values
Unlike the stack, inserting and retrieving things from the map isn't as error prone

However, the source code is less intuitive and more space than necessary is used, since nodes and values are getting copied to an external data structure that stores partial results for the entire lifetime of the program.

The Fourth Option: Retuning in the Grammar Directly

A we can specify a return value in the grammar itself with the returns keyword

expr returns [int value]
    : expr MULT expr
    | expr ADD expr
    ;

Here, int value must be using the syntax of the target language, in this case Java → less decoupling

This value will be visible as a field in the ParseRuleContext type object directly (specifically, in the subclass corresponding to the current rule, in this case ExprRuleContext). All methods that use an expr will have access to this value.

public ... ExprRuleContext extends ParserRuleContext {
    public int value;
    //...
}

V0D - Visitor and Listener Examples from Scratch (Java)

the following lecture topic involves writing a Calculator interpreter using a visitor, and a Translator using a listener, both in Java

if you're reading this, I didn't make notes on it because a) it mostly summarizes/applies things we've already covered and b) later material is more urgently needed for my midterm prep

V0E - Actions in Grammars

exhaustive list of actions, I feel like there were some in previous slides, no?

If we ~~feel insecure about our OOP knowledge and want to avoid inheritance~~ wish to forgo visitors and listeners, we can use actions to include application code in the grammar directly.

There are some cases where the computation required for our output is so light that using a visitor or listener to handle it is genuine over-optimization.

The @parser::members action adds members to the MyGrammarParser class that gets generated automatically; we may use these members later in the grammar using {} syntax to drop into our application programming language (e.g. Java).

Aside: does this java code get directly appended into the rule methods defined in the parser? Are there any other steps?
We can use this in conjunction with ANTLR constructs like locals

In this example, we parse tab \t separated lists; we want to be able to pass in a column number n to the parser and print only entries in that are in column number n.

grammar Rows;

@parser::members {
    // in here: Java
    // adds a col member to the RowsParser object
    int col;
    // we must redefine the constructor to initialize this new field
    public RowsParser(TokenStream input, int col) {
        this(input);
        this.col = col;
    }
}

// back to the grammar
file: (row NL)+;
// rule for "row" in the grammar
// we define a local variable i with locals (Java in the [])
row locals [int i = 0;] : ( /* grammar nodes etc */ STUFF {
    // in here: Java
    // we access local parameters we've defined earlier
    // and grammar nodes with $ syntax 
    $i++;
    if($i == col) System.out.println($STUFF.text);
})+ ;

// skip whitespace, etc.

Then, in the main function where we build our parser, we call the RowsParser constructor. We do not build a tree because the output is generated while the grammar is being parsed; we just call the root rule in the parser object.

public class Col {
    public static void main(String[] args) throws Exception {
        // set up the ANTLRInputStream, RowsLexer, CommonTokenStream as per usual
        // ...
        int col = 0; // read from args or whatever
        // constructor, with the col value as specified earlier
        RowsParser parser = new RowsParser(tokens, col);
        // we will NOT build the tree
        parser.setBuildParseTree(false);
        // instead, we parse the root rule, in this case file
        parser.file();
    }
}

Aside: does being able to pass arguments in like this affect the $k$ parameter of the parser and/or whether it's context-free/sensitive?

V0F - Semantic Predicates

Semantic predicates and their consequences have been a disaster for the human race

Problem statement: we want to parse a file with the following format; we want to parse the input into a list of groups.

A first integer $n_1$ which indicates that a group of $n_1$ integers will follow it
Next integers $k_1, \dots, k_{n_1}$ that form the first group
Another integer $n_2$ indicating that a group of $n_2$ integers will follow it
Etc.

Here, the structure of the parse tree depends on previous values that have been parsed.

We can implement this grammar with a semantic predicate, which is an alternative predicated on one of the values in the rule itself. It uses the {} syntax to access the implementation language, and passes a parameter into the sequence rule with [] syntax.

In this particular example, we use an iterator variable i to keep track of how many integers we have read into the group. If we still have space left in the group (i.e. if $i < n$), then the semantic predicate keeps the alternative visible. Otherwise, once we've read everything, the alternative cannot be taken anymore.
Aside: gather all these parameter passing, actions, local, fragments, etc. into one document in the ANTLR section of the notes

grammar Data;

file: group+;
// we pass the integer value of the first token into the sequence rule
group: INT sequence[$INT.int];

// sequence rule
sequence[int n]
locals [int i = 1;] : 
// match n integers
// i.e. if we haven't matched n integers yet (which we keep track of with i)
// continue to make this rule available here
// and since it's the first one, we will keep taking it
({$i <= $n}? INT {$i++;})* ;

// tokens ...

Use-case

Generally, we don't need semantic predicates, so they should be regarded like many obscure features of programming languages: if you're using it, you're probably using bad style (and should do something else) or you've structured something wrong up the chain. However, for pathological grammars, semantic predicates can clean up the specification.

Aside: what is the implication of this in terms of automata theory? How does it affect the determinism and the $k$ and the context free/sensitive of the language?

V10 - Lexical Modes and Island Grammars

An island grammar contains grammars for multiple languages in the same file. To support this, multiple lexer modes are defined; a particular rule (a sentinel character sequence) tells the lexer to switch modes and start parsing a different language.

Specifically, once a mode changes, the grammar jumps to that mode's label and starts looking there
Aside: this looks suspiciously like how functions are implemented in assembly language; I wonder how we could cheese the Turing-completeness of this system.

E.g. for an XML parser, < tells the lexer to switch into "attribute" mode, where it looks for attributes in the header of a tag instead of for other tags inside it

lexer grammar XMLLexer;

// default "mode" starts at the top of the file
OPEN: '<'                        -> pushMode(INSIDE);
COMMENT: '<!--' .*? '-->'        -> skip;
EntityRef: `&` [a-z]+ ';';
TEXT: ~('<'|'&')+;          // matches any 16-bit char except '<' and '&'

// the mode for something INSIDE a tag
mode INSIDE;

CLOSE: '>'                       -> popMode;
SLASH_CLOSE: '/>'                -> popMode;
EQUALS: '=';
// etc.

Related reading: Chapters 5 (Designing Grammars) and 6 (Exploring some real grammars) of Language Implementation Patterns.

V11 - Parsing DOT

Improve your parsing chops

DOT is a domain specific language for describing graph-theoretic visualizations. In this section we use it as an example for constructing an "actual", pragmatic grammar. A more in-depth description of the language can be found here.

Example DOT Program

digraph G {
rankdir=LR;
main[shape=box];
    // define edges main -> f and f -> g
main->f->g;
    // styled edge
f->f[style=dotted]
f->h;
}

Feature: Case-Independent Identifiers

DISGUSTANG

// tokens
STRICT:   [Ss][Tt][Rr][Ii][Cc][Tt];
GRAPH:    [Gg][Rr][Aa][Pp][Hh];

Feature: Matching Angle Brackets

DOT accepts strings of HTML, which must occur in matched pairs.

Tests reveal that some suspicious sequences are recognized by the grammar, e.g. <text>, e.g. < appearing in a comment. What's going on?

Naive Approaches

The first naive approach to this is to write a rule like

HTML_STRING: '<' .*? '>';

Remember, the lexer generated by ANTLR will match the longest possible string
So, lexed <hi> would include two HTML_STRING tokens < and > (don't worry; tags in angle brackets like this is valid in DOT)
- Note that the consumption of > in the second example is not an error; it is a result of the lexer matching to the longest possible sequence. The non-greedy loop just means that it has to end with a >.

We could also try

HTML_STRING: '<' (TAG | .)*? '>';
TAG: '<' .*? '>';

This would yield the same results because <i and /i> can be matched by ., i.e. when trying to match the longest possible sequence, the lexer sees < as a tag of type <i.

Solution

To solve this problem, we need to explicitly define that the characters < and > cannot be in the header of a tag, i.e. part of the tag name:

HTML_STRING: '<' (TAG | ~[<>])*? '>';
TAG: '<' .*? '>';

Note that implementing HTML_STRING with a recursive call to itself instead of tag would match the case <hi> properly, but would also recognize false positives, e.g. <<i >>.

V12 - Symbols and Scopes

Variables in a program are like characters in a novel Very cool and meaningful takeaway inside: "interfaces are types and types are interfaces"

Symbols

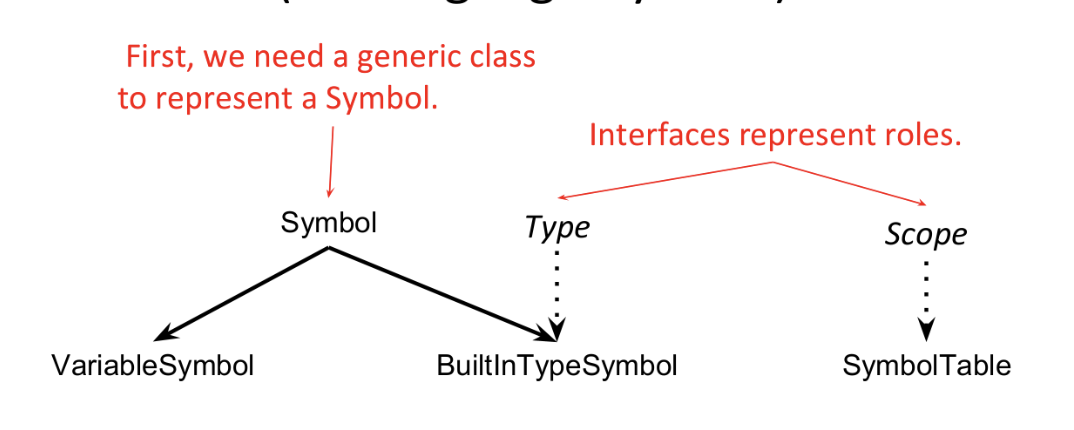
A symbol or atom in a programming language is a (the) primitive piece of data, whose form is human-readable. A symbol may be an identifier, literal, keyword, etc. A symbol table is a registry of all the current symbols in a program (the language starts with some, and more are added at runtime).

Heuristic: in most programming languages, symbols are the pieces of text separated by whitespace in the source code
Aside: some languages like LISP have "symbols" as a data type in the program itself; they usually behave similarly to enums

A symbol must have a name, a category, and a type. E.g. the symbol f in the C++ statement T f() {…} has name f, category method and type T.

Representing Symbols

We can represent a symbol in a program (presumably one that deals with other programs, like an interpreter or compiler) as a class or structure, with each attribute listed above as a field. The type of this value corresponds to the category of the symbol.

If we implement with classes, we can create new symbol objects by passing parameters into the constructor

// corresponds to "class T{...}"; we define the type T, which can be used later
// note how classT{...} is basically "define type T"
Type t = new ClassSymbol("T"); T{...};
// corresponds to f in "T f() {...}"
MethodSymbol m = new MethodSymbol("f", t);
// create a new built-in-type symbol "int" so we can declare ints
Type intType = new BuiltInTypeSymbol("int");
// correponds to x in "int x;"
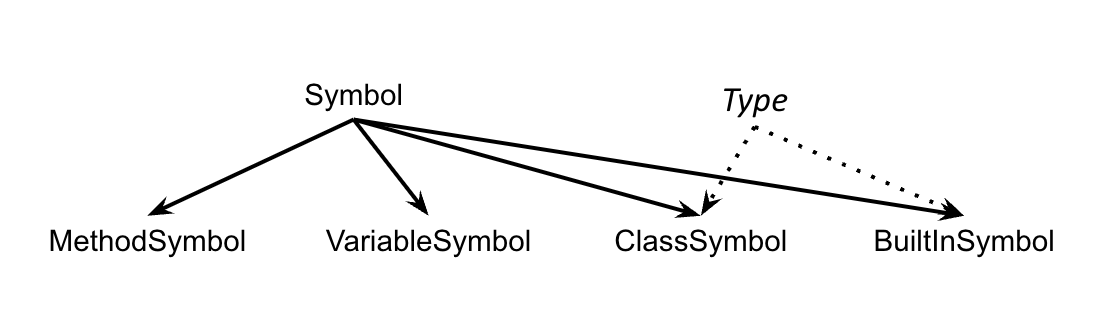
VariableSymbol v = new VariableSymbol("x", intType);

A implement a symbol table by writing a common superclass for all symbol classes. Then, we can just store an {name, Object} map (or whatever structure) of this.

public class Symbol {
    // fields needed for every symbol
    public String name;
    public Type type;
}

Representing User-defined Types

User-defined types are represented as interfaces, which act as tags that can be "added on" to program symbols. This interface characterizes user-defined types from other program symbols. Any symbol implementing this interface must be a type.

Aside: This relationship between types and interfaces is very interesting; it implies that types and interfaces are two expressions of the same thing. In particular, both interfaces and types declarations define constraints; the describe how something (a class or a value) should act.
This is the philosophy of "duck typing": if a value acts in a way described by a type, then it is of that type. So, like a value can have multiple types, so too can an object implement multiple interfaces.
Interfaces are a type system for classes

// a symbol class for a built-in type symbol
public class BuiltInTypeSymbol extends Symbol implements Type {
    // ctor
    public BuiltInTypeSymbol (String name) {
        super(name);
    }
}

// Type interface
public interface Type {
    public String getName();
}

Class Hierarchy (summary)

Scopes

A scope is a well-defined region of code that encloses symbol definitions. A lexical/static scope is a scope that can be known at compile time; usually this means scope explicitly defined by tokens in the source code. A dynamic scope is a scope that can only be known at runtime.

Alt defn: in a static scope, the same symbols will always be defined no matter when the scope is accessed. This is not true of a dynamic scope.
- Aside: this is like a pure vs. impure function. Ironically, LISP is dynamically scoped.
Static scope is preferable as it is easier to reason with and lets us make guarantees about which symbols will be defined which, which is extremely useful
Many languages delineate scope with curly braces {}, including C, C++, Java, etc.

Further Properties of Scopes

A named scope has a name (e.g. classes, methods, function definitions, etc.); some scopes aren't named (e.g. the global scope/top-level scope of the program). A nested scope is a scope that appears inside another scope; most languages allow this.

Languages can use scopes to restrict what type of code can be where. E.g. in C, statements are not allowed in structures (aside: how is this different than simply disallowing this in the grammar?)

The visibility of a scope is defined by the language, and can sometimes be defined in the language directly, i.e. with keywords like public, private, etc.

A language with a monolithic scope has a single global scope for the entire program, e.g. config files. These are best implemented with a map that matches symbol names to Symbol objects.

Representing Scopes

Like with types, we can define an interface that tags an entity as a scope. Unlike with types, more methods are needed to provide ways to interact with the scope, which we will need.

public interface Scope {
    public String getScopeName();
    // get the scope surrounding this one (possibly the global scope)
    public String getEnclosingScope();
    // create a new symbol in the scope
    public void define(Symbol sym);
    // resolve a name (string) to a symbol in the current scope
    public Symbol resolve(String name);
}

Organizing Scopes

Monolithic scopes are easy to organize; we just have one. However, multiple (and particularly nested) scopes imply a scope stack or scope tree structure for storing the scopes of a program. More on this later.

Note that "The Stack" that we are all familiar with is essentially a (the!) scope stack, in most programming languages.

should there be more here or do we cover it later?

tree ref and push and pop and stuff?

Resolving Symbols in a Scope

We resolve a symbol name by retrieving the Symbol object it refers to or determining that it is mapped to no Symbol object at all. This depends on the scope are are currently in, because the same symbol name defined or undefined (or correspond to a different object) depending on the scope.

To resolve a symbol name, we look at the associated Symbol object in the innermost scope. If we can't find it there, we check in the enclosing scope, then that scope's enclosing scope, etc.

This is why our Scope interface needs a getEnclosingScope function
Given the name of the current scope, we can always resolve the symbol (possibly to null)

public Symbol resolve(String symbol_name) {
    // look for the symbol in the current scope
    // since a scope is "monolithic within itself" (I guess),
    // we use a map to associate names to values within the scope
    Symbol s = members.get(name);
    if (s != null) return s;           // guard stmt
    // if we made it here, our scope doesn't define the symbol
    // so we recursively resolve the symbol in the enclosing scope
    if(enclosingScope != null) {
        return enclosingscope.resolve(namne);
    }
    // if we made it here, the symbol isn't defined anywhere
    return null; // or throw an error or something
}

for later: what a data aggregate IS is to expose its inner scope through its own namespace

a struct is both a type and a scope, this is what aggregates are

arith result table looks like a group mult table

V13 - A Monolithic Symbol Table

The Grammar of Cymbol

We define a language Cymbol with the following grammar to illustrate concepts relating to symbols and scoping; its syntax is similar to C, hence the name. We just define the grammar here, we don't put anything (e.g. annotations?) in it.

grammar Cymbol;

// a declaration may include a definition, or not
varDeclaration : type ID ('=' expression)? ';';
// only number types
type: 'float' | 'int';
// expressions
expr: primary_expr ('+' primary_expr)* ;
primary_expr: ID | INT | '(' expr ')';

// tokens
ID: LETTER (LETTER | '0'..'9')*;
fragment
LETTER: [a-zA-Z];
INT: [0-9]+;
// hidden
WS: (' '|'\r'|'\t'|'\n') {$channel=HIDDEN;};
SL_COMMENT: '//' ~('\r'|'\n')* '\r'? '\n' {$channel=HIDDEN;} ;

So our resulting classes are organized like this

Code (Java)

We can construct a symbol with a name, or with a name and a type; so, the Symbol class has two constructors, once of which has an additional this.type = type; line. We also define getName() and toString() functions.

code in here later

Symbol is extended by two subclasses: VariableSymbol, which simply calls super, and BuiltInTypeSymbol, which implements Type.

We create a SymbolTable object as a dictionary to hold the symbols. If this symbol table is monolithic, our scope tree only has a single node, so we can use the symbol table to implement scope as well (correctness?).

import java.util.*;

public class SymbolTable implements Scope {
    // data structure to hold the dictionary
    Map<String, Symbol> symbols = new HashMap<String, Symbol>();
    // ctor
    public SymbolTable() { initTypeSystem(); }
    // initiate the type system:
    // create symbols for built-in types that need to exist immediately
    public void initTypeSystem() {
        // note: define is a function implemented in this class
        define(new BuiltInTypeSymbol("int"));
        define(new BuiltInTypeSymbol("float"));
        // etc.
    }
    
    // symbol table is in the global scope -> nothing enclosing
    public String getScopeName() { return "global"; }
    public Scope getEnclosingScope() { return null; }
    // add a new symbol to the symbol table
    public void define(Symbol sym) { symbols.put(sym.name, sym); }
    // resolve a symbol (remember, monolithic scope, so no recursion necessary)
    public Symbol resolve(String name) { return symbols.get(name); }
    // toString()
    public String toString() { /* ... */ }
}

If we follow the ANTLR3 way of doing this, we will need to access the symbol table in the grammar directly in order to resolve symbols

grammar Cymbol;
@members { SymbolTable sym_tab ;}     // remember, this is Java code inside {}
// compilationUnit is the start (root) rule
// we pass the symbol table to it as a parameter
compilationUnit[SymbolTable sym_tab]
// on start up, initialize the symbol table
// aside: does this mean @init places the code in the block into the ctor?
@init { this.sym_tab = sym_tab; }
// now we can define the alternatives for the compilation unit rule
: varDeclaration+ ;

In the type rule, we must resolve the type symbol from the name in the grammar (using the symbol table), then return the specific type symbol (ANTLR has a returns keyword!! also @after is executed just before the block returns)

type returns [Type type_sym]
@after {
    System.out.println("line" + $start.getLine() + ": ref" + $type_sym.getName());
}
    // syntactic predicate?? check
    : 'float' {$type_sym = (Type)sym_tab.resolve("float"); }
    | 'int' {$type_sym = (Type)sym_tab.resolve("int"); } ;

varDeclaration rules require adding a symbol to the symbol table by calling define. We must use the type_sym that was returned by the Type rule (this would have happened right before).

Aside: in ANTLR, where does stuff get returned to? Is there a stack somewhere? Hello?

Then, when we reach an ID (identifier), we resolve it in the symbol table.

Code (C++)

The grammar remains clean.

We make a lot of shared pointers shared_ptr in the C++ code. Why? We always declare them when we pass in things (or declare fields) like Type objects. Why shared pointers? Review cpp.

todo: compile the entire grammar into a code file, maybe external

V14 - Nested Scopes

E.g. methods have two scopes: one "outer" scope that includes the parameters of the method, and one "inner" scope that includes the parameters of the method and the local variables defined inside the method. These scopes are nested.

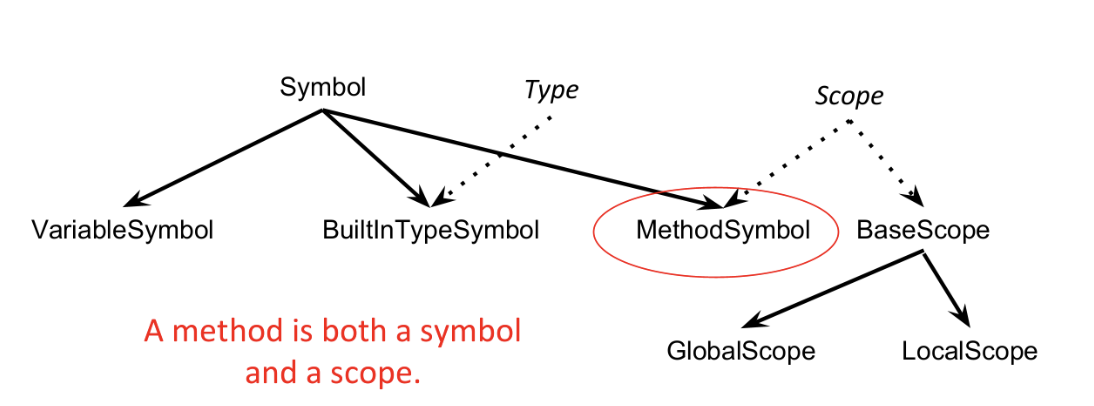
Thus, a method is both a symbol and a scope.
We re-arrange the class structure a bit to add methods:

Note we've separated scopes into "base" and "user-defined" (i.e. methods), and further separated "base" into the global scope and local scope(s), e.g. anything created with {}, which is a core language feature.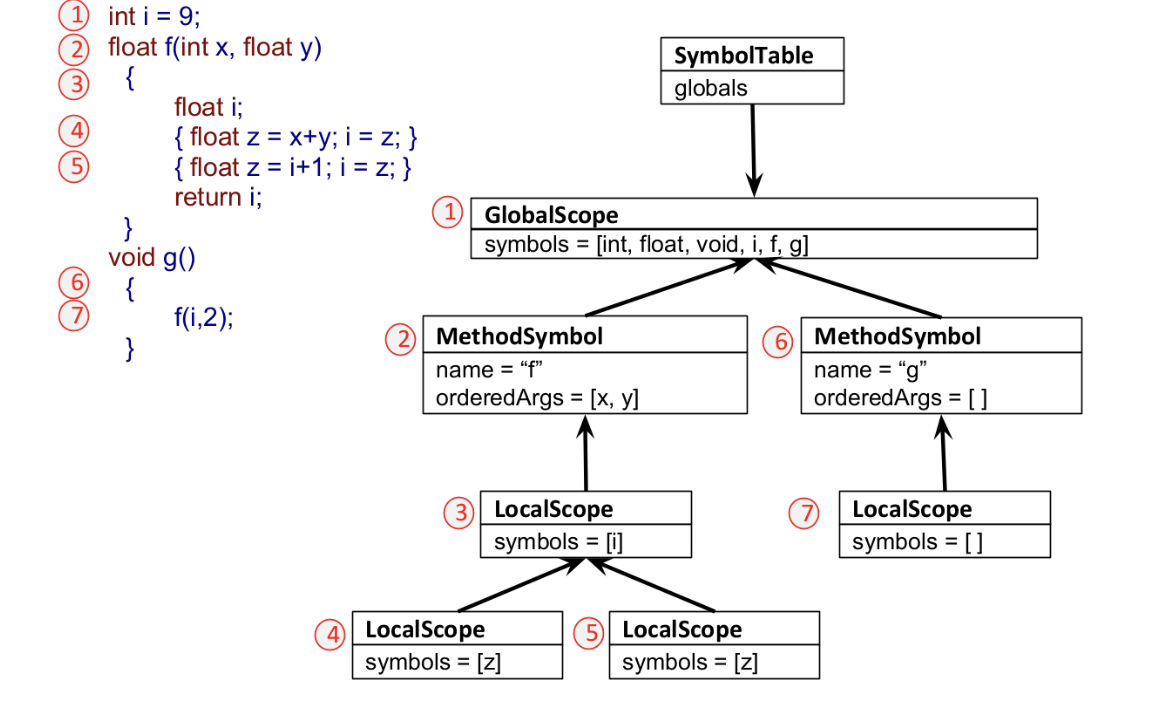

Scope Tree Example

The Software Engineering behind it terrible title

In ANTLR3, our symbol table construction happened in the grammar directly, with annotations? the things with @ being triggered by the grammar rules.

We can also trigger this actions while walking over an AST created from the input source code; this adds an extra pass that allows us to further decouple the grammar from the application code.

So, instead of building the classes in the grammar, we embed the AST construction code in the grammar instead.
Then, when walking the AST, we populate the symbol table and resolve variables and method references. We trigger these actions using tree pattern-action pairs. bold this? or italics

In ANTLR4, the idiomatic way to do this is to trigger actions while using a visitor to visit the parse tree.

Temp Aside: What the Fuck Are Symbol Table Actions?

as we walk along the parse tree or an AST, we interact with the symbol table. We can characterize these interactions in 4 ways:

def: we define something new that requires a new symbol, e.g. method
- E.g. (def) VAR_DECL, (def) PARAMETER, (def) METHOD_DECL
- Defining something in the current scope
- This includes defining all the BuiltInType stuff in the global scope
ref: we reference a user-defined symbol that's already in the symbol table, e.g. an identifier, a method symbol, etc.
- this appears to happen after we get to the symbol in question in the tree
- These seem to be the only cases, e.g. built-in types aren't refed → BUT THEY ARE IN LATER SLIDES HUH??????!!
push and pop: we push and pop scopes from the scope stack/tree.
- This happens once every time we see a BLOCK: it looks like (push) BLOCK (pop)
- As mentioned, this happens twice for method declarations: (def) (push) METHOD_DECL (pop) for the scope with parameters, then exactly one level down, (push) BLOCK (pop) for the block
- Aside: notice how sometimes we dont need blocks for if statemetns and loops: this just means we don't create a scope inside of it! So it's not just a code style thing: it is genuinely different. However, I dont think we can omit them with methods even if we dont declare local variables (Check)

When annotating these actions on a AST diagram, the order matters, e.g. we always push before we pop. Things before the AST node text happen before we descend into the tree and things after happen on the way back up; this structure mirrors a listener.

E.g. (def) (push) METHOD_DECL (pop)

The order is always a subset of (def) (push) NODE_NAME (pop) (ref)

Tree Pattern-action Pairs

E.g. for a BLOCK rule, we create two rules that match it: enterBlock and exitBlock, both of which are just defined as : BLOCK;. In the enterBlock rule, we define whatever code action we want when entering a block (e.g. pushing, i.e. creating a new local scope) by writing that code directly in the grammar with the {} syntax, then the same on the way out.

tree grammar?

tree grammar DefRef

enterBlock : BLOCK {
    // we create a new local scope
    // current scope as a parameter so we know what to affix it to
    // set this new scope to the current scope
    currentScope = new LocalScope(currentScope);
};

exitblock: BLOCK {
    // pop the local scope by setting the current scope to its enclosing scope
    currentScope = currentScope.getEnclosingScope();
}

Since both rules match BLOCK in exactly the same way, we need additional infrstructure to make sure the right one is called. We define block topdown and bottomup rules; each one lists all the rules for "on the way in" and "on the way out" as alternatives, respectively.

topdown: enterBlock | enterMethod | ... ;
bottomUp: exitBlock | exitMethod | ... ;

E.g. Methods

code

when we enter a method, we made a new method symbol (using the return type returned by the Type rule before (?)) Type retType = $type.type_sym; in the current scope, call currentScope.define(our_method_sym) on this new rule, and finally set currentScope = our_method_sym to define the current scope as the method symbol (since the method symbol is a scope).

Then, on exit, we simply set currentScope to its enclosing scope

Building the Scope Tree C++

code

defRef class, visitMETHOD_DECL in our implementation:
get the std::shared_ptr<AST> ty and id for the type symbol and identifier from the parameter t (the AST node representing the method declaration itself); it is the first and second child.
print out that weve defined a method with getLine()
resolve the type ty and define it as the return type (a shared pointer of type Type)
make a shared pointer ms with std::make_shared<MethodSymbol>(…) where we pass in id->token->getText() to get the name of the symbol, the return type we just made, and the current scope.
call currentScope->define(ms) to define the method in the current (global) scope
set currentScope = ms (this is our new current scope)
visit the children of t
Then, when we're done, set currentScope = currentScope->getEnclosingScope(), which pops the method scope
Aside: note: currentScope appears to be a field of the parent class, we've been accessing it everywhere
- Remember, the object were in implements scope so we can do all this stuff

when in doubt, the type is std::shared_ptr<AST>

visitDECL

create the sharedPointer<AST> vars from the parameter to get the type and the id t->children[0], t->children[1]
print whatever
resolve the type into a shared_ptr<Type> type = resolveType(ty)
we define a shared ptr to a new variable symbol vs with std::make_shared<VariableSymbol>(id->token->getText(), type);
define in current scope currentScope->define(vs);
then visit the children of t (the input pamater that is an AST node)
We dont make a new scope, since we're just declaring a variable, which doesn't have its own scope

V15 - managing Symbol Tables for Data Aggregates

A data aggregate supports access to multiple fields, e.g. a struct; essentially, a data aggregate encloses its own scope. A class is a type of data aggregate that also allows function definitions within that scope, and may have superclasses as well.

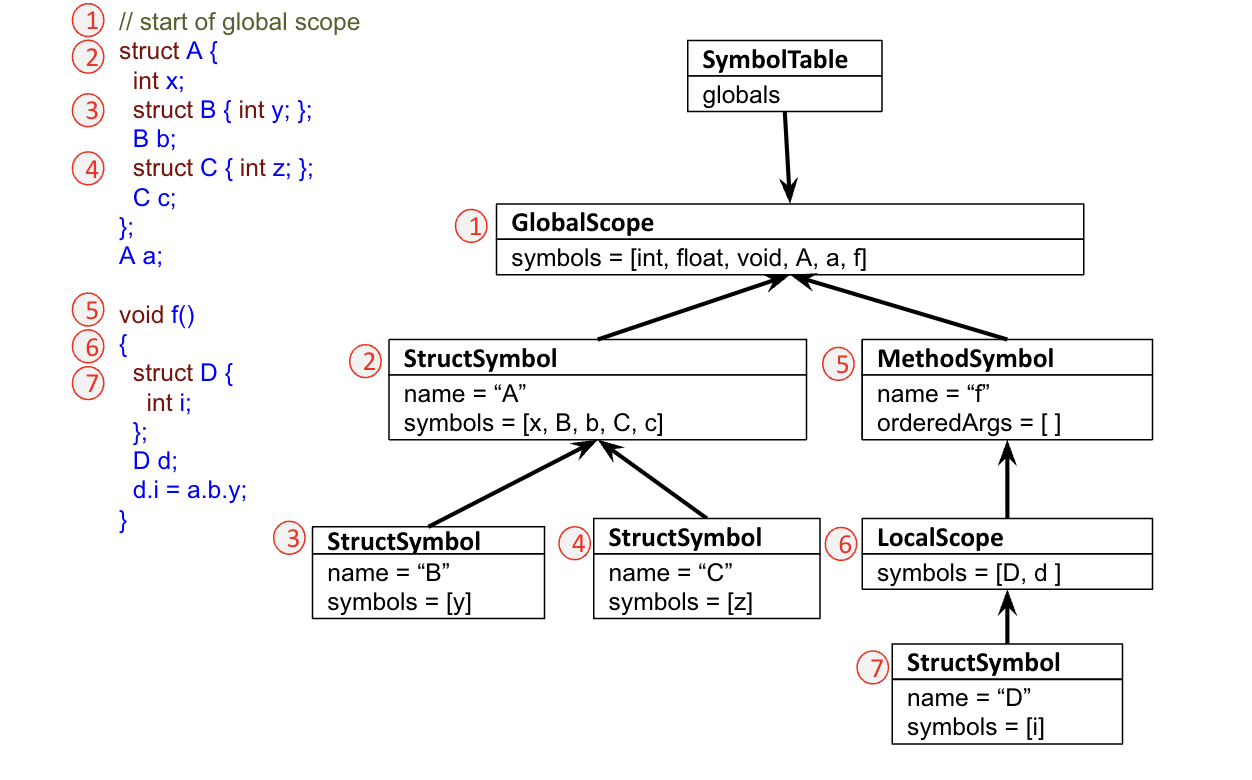
By definition, code outside the data aggregate scope should be able to access members inside of it; this requires special attention to their scope implementation.

Scope Tree Example for Data Aggregates

Things of note (maybe move this somewhere else when needed): all the "keywords" are defined in the global scope here! The symbol table points to the global scope just like the other symbols do. Remember that all the symbols defined belong in the scope, so Struct B {int y}; B b; adds symbols B and y, but also b. Things defined with BLOCK i.e {} are of type LocalScope
Aside: method args are ordered struct sumbols aren't. Is this a defining difference, i.e. methods are scopes whose arguments order matter and structs aren't (ties into the lisp thing below?)? flesh out this idea.
When resolving, we use a stack to track where we are. we should move into the right place (i.e. struct scope)

When resolving struct symbols, we cannot walk up the tree! This could cause us to resolve to the wrong variable. Instead, we should find the expression in the scope of the structure, or return "no such field" indicating an error.

Since we do need to walk up the tree (i.e. look in enclosing scope) to resolve normal symbols, we need different resolve methods for base and member references.
We have resolve for base references and resolveMember for members.
I.e. the fields of a struct are tightly bound to that struct, so if they share a name with something in the enclosing scope, it's never that thing in the enclosoing scope, evne if its not defined in the struct

Scope Tree Example for Classes

Before looking in the global scope, we must look up the inheritance chain. So, if a symbol is not defined within the scope of a class, we look to see if it's defined in the scope of the parent class. The ability to do this is what fundamentally differentiates classes from structs.

diagram from slides?

Forward References

A forward reference involves defining a variable before declaring it. They are used to tell the compiler that a variable will exist (and thus it can be referenced), but just hasn't been defined yet.

E.g. void main() { x = 10; } /* maybe some more code */ int x;
E.g. we see this with function in Java: we can access a helper function in a main class, then define it after that main class in the file.
It is named as such because we must look forward in the program to find the definition

We can implement forward references by running two passes through the AST: one for defining symbols, then one for resolving them.

Since every forwardly referenced symbol will be defined after the first pass, it will resolve to something in second pass (assuming the scopes line up and no errors were made, etc.)

Forward references are not allowed in cymbol outside of a class. We can detect illegal forward references by examining what they resolve to in the resolution pass. E.g. in cymbol, if the forward reference resolves to a local or global symbol, it's illegal, but if it resolves to a field in the same class, it's fine.

New Class Hierarchy

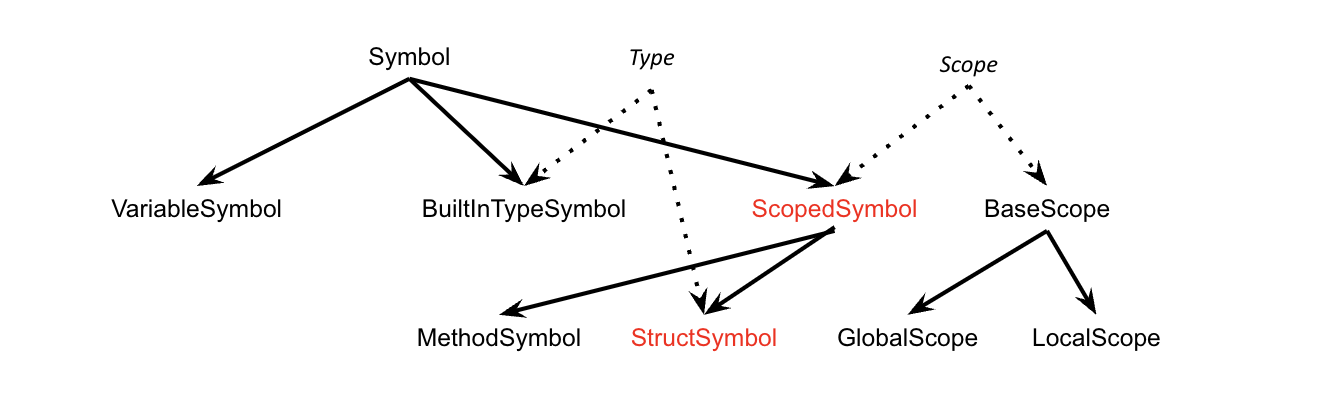
ScopedSymbol is an abstract ish class: it is used to categorize the types of scoped symbolss, i.e. MethodSymbols and StructSymbols. We need to differentiate these because only StructSymbols can be types; structs are types, but methods are not.

members in the grammar

Aside: we use an optional rule for defining member int he grammar ^('.' member ID) (^ indicates an AST construction rule).

Problem: also matches to a single id

Aside: just how in lisp we can implement structs (and local scopes in general) with lambda functions (and vice versa), can we simply desugar all data aggregates to methods if we want?

V16 - Class Symbols

We store information in the AST nodes: the resolve pass needs the current scope computed in the first pass, so we store that in the corresponding AST node.

Variable declaration int x; in the main method of a class

(def) x as a variable symbol (object, sym) in the current scope
set the sym.def to the AST node of x
set the ID AST node's symbol to sym
set the scope field of x's return type AST node to the current scope
set the scope of x to the current scope

multipel passes:

set token stream
make a common tree adaptor that creates the ast
set the start rule
make symbol table
init the suymbol table
create a def pass
do pass 1 with downup
reset nodes: rewind the AST node stream to the root so we can do another pass
create a ref pass Ref ref= new Ref
run the def pass (pass 2) with downup

V17 - Type promotion

we need to figure out the result types given the input tupes

eval type: oroginal type
promoteToType : the type we promote to (if they're the same or we dont promote, we just use null → tells us to use orignnianl)

create type indexes as public static final int tTYPENAME = n for ascending $n\in \mathbb{N}$

Create a result table where we can look up the result of type promotions

type computation: look at the AST, get eval types (get the index as an int), look up the result in the table, call propmoteTypeType from the on the type to the result (if its null it just ignores so we can always call it)

where do we need to promote

arguments of method calls
variable declaration
return statement
assignment

semantic predicates have syntax {}? and start at the front, if its true the alternative is there, false its not

lexer predicates (are these synytactic prediactes?) are for lexer rules and appear at the end of the lexer rules. They only create the token if the thing is true. Still {}? synatx.

we can reference previously parsed withngs with input?? somehow

A DFA is genreated

ANTLR 4: for pathological stuff, we just check if the ID is whatever as a parser rule with alternatives: id: 'if' | 'for | ... keywords | ID, then ID token is parsed as normal. ANTLR4 makes this work!

Non-deterministic rule → deterministic rule: semantic predicates!

syntactic predicate vs. LL* uses a DFA not a pushdown and cannot regonzie mathcing parnetihtses? examines future inpout symbols for a rule

sematnic prediates for specifying which ambiguous alternatieve to pick. ANTLR 4 does't need this because its LL star

we can solve ambiguity by left factoring

V19 - Type Safety

An operation must be defined for the types of its operands

I.e. we need to be able to look up a definition of the operator for the combinations of types for the operands
So, the operands need to match a definition of the operator exactly, or some of them need to be type promoted to a matching definition

Static Type Safety

Different operators impose different type requirements

The dot operator . requires the left operand to be a struct
The if(expr) block operator requires expr to be of a boolean type
The assignment operator = (in lh_val = rh_val) requires lh_val to be an l-value and that lh_val and rh_val are the same type (or are promotable to the same type)

We can define a result table/type table where we can lookup the resulting type based on the type of the operands. We also define a type promotion table to lookup what type promotion we should define, given the two operand types.

If we have an operation between an integer and a char, we can lookup typeTable[tChar][tInt]

Implementing Type Enforcement

Since this kind of type checking is static, we can implement it as an AST pass. Thus, our lookup function is performed on two ASTs:

public Type getResultType(AST a, AST b) {
    // get the type indices of the operands
    int t_a = a.evalType.getTypeIndex();
    int t_b = b.evalType.getTypeIndex();
    // look up the resulting type from the table
    // typeTable is a static member of the overarching class
    Type result = typeTable[t_a][t_b];
    // if there is no entry, then something has gone wrong -> error
    if(result == t_void) {
        // throw error
        // bleh
    }
    // since an entry exists, we lookup the type promotions
    // note: if no promotion is necessary, the lookup just returns 
    // the original value
    // so, as a point of SWE, we just always perform the lookup
    a.promoteToType = promoteFromTo[t_a][t_b];
    b.promoteToType = promoteFromTo[t_b][t_a];
    // return the resulting type
    return result;
}

Polymorphic Type Safety

Under the model of polymorphism, an object may have multiple types, corresponding the members of the leaf → root path of the inheritance tree.

Aside: this illustrates the "type as an interface" idea: a type just guarantees that a value will "act" in a certain way, much like an interface does. Nothing here prevents an object from acting in a way that satisfies multiple type definitions. Thus, under the duck typing interpretation, the value may have multiple types.

Polymorphic Assignments

We are allowed to assign an subclass object to a superclass object, but not a superclass object to a subclass object.

This is because a subclass object is also a superclass object, by definition. The subclass is a superset of the interface of the superclass; the superclass is the restriction of the type interface to the shared "endpoints" of all objects
Reference type vs. Object type

So, when doing polymorphic type checking, we must check whether the classes are the same. If they aren't, we must check if the l-value is a superclass of the r-value.

Animal *animal_1, *animal_2;
Dog* my_dog;
Cat* my_cat;

// Example assignments
animal_1 = animal_2;     // fine: both are Animal
animal_2 = my_dog;       // fine: Dog is a subclass of Animal
animal_2 = my_cat;       // illegal: Animal might not be a Cat
my_dog = my_cat;         // illegal: Dog is definitely not a Cat

We define a canAssignTo function (analogous to the getResultType function earlier) to check whether a polymorphic assignment can happen.

We can add this function to our type interface

Note on Pointers

This is more less enough to implement type checking for pointers. If the pointer points to a value (e.g. an int), then we check the type table / promotion table. Otherwise, if the pointers are to objects, we perform the polymorphic type checking.

Pointer Arithmetic

Uh oh

If we are allowed to mutate pointers like values themselves, we must add them as indices in our type table. By definition, if we implement pointer arithmetic, we can operate on pointers with integers, for example.

Summary

Static type checking happens in 3 parts correctness

Type computation: which types are involved in the operation
Type promotion: do some types need to be promoted
Type checking: do the types match?

V1A - Predicated Parsing usage

Recall: a semantic predicate lets us "block" an alternative in a grammar rule by computing a boolean expression based on information available at parse-time.

When Should We Use Semantic Predicates

Can be used to extend existing grammars to support multiple versions. E.g. if we have a Java 4 grammar and want a Java 5 grammar, we can couple them and simply have a boolean variable that indicates which version we are parsing against. Then, certain alternatives can be blocked via a semantic predicate if they are not part of that version.

Syntax: rule : {bool_expr}? alternative_1 | alternative_2

We can also define lexer predicates that do the same thing, but in the lexer instead. In this case, the predicate is placed at the end of the lexer rule.

Lexer rules don't have alternatives, so the predicate determines whether the lexer rule acts at all
Syntax: TOKEN : /* pattern */ {boolExpr}?

Examples

Use case: using keywords as variables

ANTLR3: define parse rules for each overlap keyword/identifier. Use a semantic predicate to check if we are in the case where the token is actually used as a keyword. If not, parse as an identifier. Gross
ANTLR4: in the grammar, we lex keywords and identifiers as normal (i.e. keywords before identifiers). In the grammar, we handle the rules with keywords first. Then, we have an identifier parse rule that looks something like id : 'keyword1' | 'keyword2' | ID, where ID is our identifier token from the lexer. ANTLR4 knows to look for the keyword uses first.

Use case: different uses for same token

E.g. ( being used for grouping and for function calls
E.g. […] being used for array access and method calls (Ruby)
- Here, we may have non-determinism: A[1] might be access index 1 of array A, or a call to method A with single argument 1. We simply can't know without more context; we need a semantic predicate to provide this context by checking whether A is an array or not. So, the parse rules arrayIndex and methodCall will have a semantic predicate to check.

Syntactic vs. Semantic Predicates

A syntactic predicate examines future input symbols in the token stream; it lets us parse different based on what comes after the current token.

ANTLR 3 needed them to allow selection between two ambiguous alternatives. This can be done instead of left-factoring.
ANTLR 4 does not need syntactic predicates because of its LL(*) magic; it performs left-factoring automatically.

A semantic predicate lets us define a "mini-rule" that ANTLR will try to match to first. If it matches successfully, we choose that alternative. Otherwise, we ignore it.

E.g. s : (expr '%') => expr '%' | expr '!'. Here, expr '%' is the mini-expression we try to match to.

We can specify auto-backtracking as an option; this tells ANTLR to insert syntactic predicates on the left edge of every alternative. This gets invoked when ambiguity arises.

grammar x;
options {backtrack=true;}

A semantic predicate lets us test any (programmer-defined) expression we want; we can access global state and provide additional context about what we are parsing.

This makes the parser stronger

V1B - Error Handling in Parsers

What if a sentence just doesn't match the grammar?

Examples of common errors:

Mismatched token, e.g. a left-paren without a right-paren
Sentence didn't match any alternatives
A "loop" (…)+ was exited early

V27 - Control Flow Graphs

Basic Blocks

A basic block of a program is a contiguous region of the program's instructions such that

Only the first instruction can be the target of a branch
Only the last instruction can be a branch

A program can be partitioned into basic blocks.

So, we know that if one statement in the basic block is executed, then all of the statements in the basic block will be executed as well. This makes basic blocks the atomic "unit" with which to construct larger program structures.

Note: it is common for basic blocks to be only one instruction of the program.

Note: each control flow structure is characterized by the structure of the basic blocks it forms. E.g. if statements have $2$ basic blocks: the block that computes the condition, and the block that runs if it is true. if-else statements have $3$. Loops have more, but vary depending on implementation.

Aside: in many languages, blocks (not basic blocks) are delimited with {} or similar. These operate at a higher level than basic blocks, but follow a similar idea (blocks are basic blocks of basic blocks).

Algorithm for Finding Basic Blocks

Determine the leader statements (i.e. first statements) of the program: a leader statement is an instruction that
- Is the first instruction of the program
- Is a target of a branch
- Immediately follows a branch or return statement
Determine the last statements of the blocks; these are the last statements before leaders and the last statement of the program

Control Flow Graphs (CFGs)

A control flow graph is a directed multigraph $G$ where

The vertices $V(G)$ are formed of the basic block of a program
An arc exists between vertices $A$ and $B$ if it is possible that the program's control point may move directly from block $A$ to block $B$
- A vertex might have multiple outgoing arcs (i.e. if it ends with a branch) and/or multiple incoming arcs

So, any possible execution of the program corresponds to a start → end path through the CFG.

V28 - Loops and Dominance

A flow graph $G$ is a multigraph with node-set $V(G)$, edge-set $E(G)$, and a starting node $s\in V(G)$. For $a, b\in V(G)$, we say $a$ dominates $b$ if and only if every path from $s$ to $b$ travels through $a$.

Thus, domination is a relation on $V(G)$, i.e. $R_\text{dom}\subseteq V(G)\times V(G)$.
- It turns out that domination is a partial order relation, so it defines a lattice over $G$.
We define dominator set $\text{dom}(b)$ of $b$ as the set of nodes that dominates $b$
By definition, each node dominates itself, i.e. $b\in \text{dom}(b)$ is an identity.
We say $a$ directly dominates $b$ if there is no $c\in V(G)$ such that $a$ dominates $c$ and $c$ dominates $b$, i.e. every dominator of $b$ dominates $a$ (correctness).

A dominator tree $T_G$ of graph $G$ is a subtree of $G$ with root $s$. If node $a$ dominates node $b$ in $G$, then $b$ is a descendant of $a$ in $T_G$.

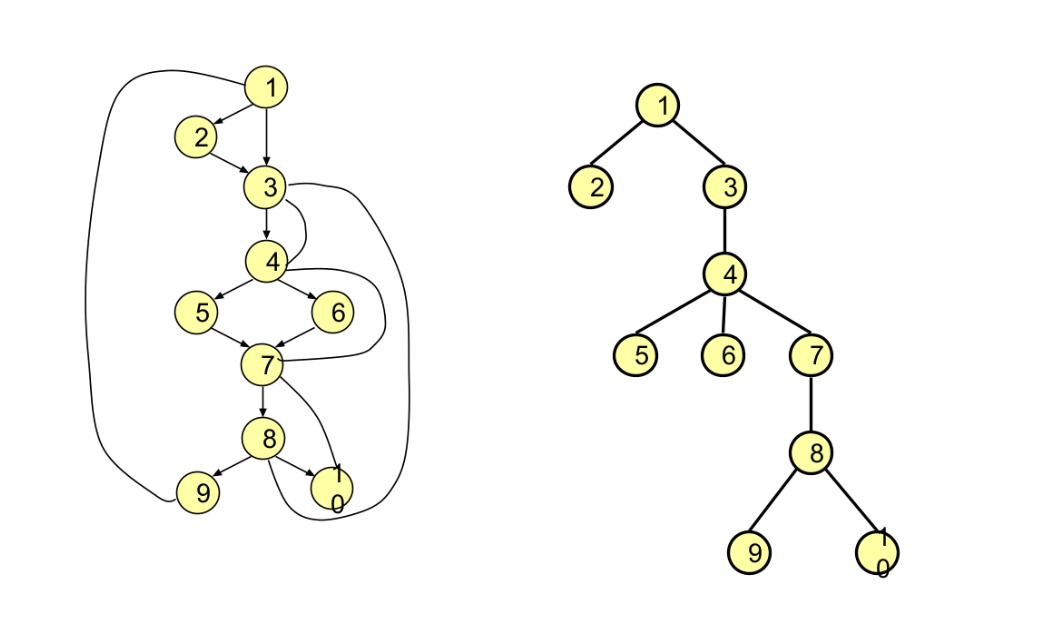
own example

Finding Loops

Heuristically, programs spend most of their execution time in loops, so optimizing loops has a higher payoff, and is thus worth spending more time on. So, it makes sense to develop a way to locate loops in a program independently of the syntax used to declare then (e.g. for vs. while vs. goto, etc.).

It turns graph theory has tools for this, and characterizing our program as a CFG lets us use them.

A strongly-connected component of graph $G$ is a subgraph $G'$ of $G$ such that a path exists between any two nodes in $G'$ (thus, these partition $G$). A loop is a strongly connected component $G'_\ell$ such that the starting node $s_\ell$ of $G'_\ell$ dominates all the nodes of $G'_\ell$.

A back edge is an edge $(b, a)\in V(G)$ such that $a$ dominates $b$ in $G$. The existence of a back edge implies a loop with the back edge in it.

These loops are called natural loops.

example (homework?)

Regions

A region $R$ of $G$ is is a subset of $V(G)$ including a start node where

The start node dominates every node in the region
Every edge between nodes in $R$ are part of the region

A single-entry-single-exit (SESE) region has a single entry and single exit, i.e. the entry dominates the region and the exit post-dominates the region.

A loop is a type of region where the region is also a strongly-connected component of $G$. So, loops can only have one entry, but they may have multiple exits.

V29 - Data Flow Analysis - Points and Paths

A point in a basic block is a location in the program that is between two statements, before the first statement, or after the last statement. A path is a sequence of points corresponding to a (graph-theoretic) path through the CFG.

In data flow analysis, we track how values are defined and used at different points of the program. This lets us implement optimizations including

Constant folding: replacing variables that have been defined but not mutated with constants
Dead code elimination: pruning code that can never be reached
Redundant computation elimination
Code motion
Induction-variable elimination (optimizes loops)
Data-dependance-graph construction

In the instruction (line n) A = B + C, we have defined A and have used B and C. We say line $n$ defines and uses these variables.

A definition $d_1$ of variable $v$ is killed between points $p_1$ and $p_2$ if every path from $p_1$ to $p_2$ contains another definition of $v$; $d_1$ is simply "visible" anymore. Otherwise, $d_1$ has reached point $p_2$ from $p_1$ (i.e. a path $p_1 \to p_2$ exists where $d_1$ is not redefined).

An expression $x\, \square \, y$ is available at point $p$ if every path from the start node to $p$ evaluates $x\, \square \,y$, and no assignments are made to $x$ or $y$ after the last evaluation of $x\, \square \,y$. Otherwise, the basic block of $p$ kills $x\, \square \,y$.

This matters because we can find redundant expressions; i.e. expressions that don't get used anywhere.
We can also find expressions that get re-computed.

We define a def-use chain as a list of all uses that can be reached by a given definition of a variable. We define a use-def chain as a list of all definitions that can reach a given use of a variable.

These make finding the use and definitions sites of variables more efficient; we need to do this often in dataflow analysis
In SSA form, we don't need to maintain these because all the definitions are at the start of the program/block, and each variable is defined exactly once there.

V2A - Reach Definitions

How do we know which definitions have reached a point in the program?

The Dataflow Equations

Let $S$ be a statement. We define

$\text{out}[S]$ as the *set of definitions that reach the end of statement $S$
$\text{in}[S]$ as the set of definitions that reach the start of $S$
$\text{def}[S]$ (or $\text{gen[S]}$) as the set of definitions that happen in $S$
$\text{use}[S]$ (or $\text{kill}[S]$) as the set of variables that are used in $S$ before they are redefined

Then, every block in the program obeys the dataflow equations:

Dataflow equations

Equation

For block $B$, we have $\text{out}[B]=\text{def[B]}\cup \set{\text{in}[B]\setminus\text{use}[B]}$ and in $\text{in}[B]=\displaystyle\bigcup_{B_P\in P(B)}\text{out}[B_P]$, where $P(B)$ is the predecessor function that lists all the blocks that lead to $B$.

Note: these are actually characterized over a lattice (??), where we use join and stuff. Look into this.

Applying the Dataflow Equations

Notice that $\text{in}[B]$ depends on $\text{out}[B]$, but $\text{out}[B]$ depends on $\text{in}[B]$. Thus, these equations describe a dynamic system (??), so we need to apply the equations iteratively until we reach a stable point.

Since these form a lattice, a theorem guarantees that we will eventually find a fixed point, i.e. a stable point.
Intuitively, the size of $\text{out}[B]$ never decreases, so there are so many "increasing" steps that can happen for other sets
Empirically, for real programs, no more than $5$ iterations are needed to reach a fixed point

To find definitions, we compute $\text{def}$ and $\text{use}$ for each basic block ($O(1)$). Then, for each basic block $B$, we initialize $\text{in}[B]$ to $\emptyset$ and $\text{out}[B]=\text{def[B]}$. Then, we iterate the dataflow equations until we reach a fixed point.

Commonly, we represent the variables as a bit vector $\in \set{0,1}^n$, where $n$ is the number of variables in the program.

V2B - Static Single Assignment

Under static single assignment form (SSA), each variable of a program is only defined once in the program's text.

Dataflow analysis is much simpler in SSA; use-def and def-use chains are not needed. SSA also simplifies the construction of interference graphs (??)
Note: this definition can be in a loop, so a variable can still be dynamically defined

Generally, SSA prevents a value from propagating (i.e. continuing to exist) in a part of the program that doesn't need it. If $p$ definitions need to be propagated to $q$, SSA form can reduce the edge count from $pq$ to $p+q$.

If a variable is assigned to more than once, we need to split each assignment into a different variable when converting to SSA form; which variable we use for a given use depends on which path we took to get to the current point (i.e. which definition we used). If the current point's block has multiple in-edges (i.e. is a control-flow path merge), this might be unknowable without actually evaluating the program.

We can define a phi function to abstract away our need to figure out which variable to use:

E.g. variable $a$ has $2$ assignments, so we split it into $a_1$ and $a_2$. Then, when we evaluate $c:=a+b$, instead of figuring out which $a$ to use (which we might not be able to know), we write $c:=\Phi(a_1, a_2)+b$. We treat $\Phi$ as being able to pick between $a_1$ and $a_2$.
Aside: this reminds me of Skolem functions in formal logic

Note: In practice, we always define phi functions in this case, even if it turns out we don't ever use the variable. We just assume dead-code elimination will get rid of unnecessary phi functions later; this simplifies the process.

Note: since we define all the variables at the start of the program, all SSA programs start with a list of undefined variables (i.e. all the program's variables get assigned "undefined"). This still happens if the first line of the program is a definition; that becomes another split variable.

V2C - Some History of SSA

1991: Efficiently Computing Static Single Assignment Form and the Control Dependence Graph is published. 1990 is the start of modern SSA.

Earlier primordial ideas are present in The representation of Algorithms from 1969.

V2D - Phi Functions

Criteria for Inserting $\Phi$ Functions

Naively, we can insert a phi function at every join point of the program (lattices?), i.e. every block that has more than one predecessor. This is very wasteful; we aren't even considering the variables themselves at all.

We only need a phi function when

We are at a join point $z$
There are two definitions of a variable $a$ that can both reach $z$ through different paths

Under the path convergence criterion, we insert a phi function for variable $a$ at node $z$ if all the below conditions are true:

A block $x$ defines defines $a$
A block $y$ such that $y\ne x$ defines $a$
Paths $x\to z$ and $y\to z$ exist
All paths $x\to z$ and $y\to z$ don't have any nodes in common other than $z$ (this is a "reduction to canonical form" step that makes sure we don't add the "same" phi function multiple times)
$z$ does not appear in both $x\to z$ and $y\to z$ prior to the end (it may appear in just 1)

Notice that, much like the dataflow equations, the PCC modifies the data it analyzes (i.e. by inserting phi functions in it). Thus, we need to apply it iteratively until we reach a fixed point.

This is really expensive, especially the path-searching part

SSA Conversion Problem

do we need to know these??

Strategies for SSA conversion algorithms:

Two-phase algorithms: build the entire dominance frontier graph (??), then find all the nodes reachable from the start. This is simple, but the DF graph might be really big
Lock-step algorithms: the reachability computation is performed iteratively while the DF relation is computed. We don't store the graph, which saves space. But, it is inefficient when computing many variables
Lazy algorithms: lazily compute the part of the DF graph that is needed; we select this part early. So, two-phase is just a spacial (extreme) case of this where we have to compute the whole thing.

Additionally, many algorithms exist for computing the dominator tree.

V2E - Dominance and SSA

In SSA, definitions always dominate uses: a variable is always defined before it is used, no matter where in the program it is or what path it took to get there.

If $x$ is used in a phi function in block $n$, then every definition of $x$ dominates every predecessor of block $n$
If $x$ is used outside a phi function, its definition dominates $n$

The dominance frontier $\text{DF}[x]$ of node $x\in V(G)$ is the set of nodes $w\in V(G)$ such that $x$ dominates a predecessor of $w$, but where $x$ does not strictly dominate $w$ itself.

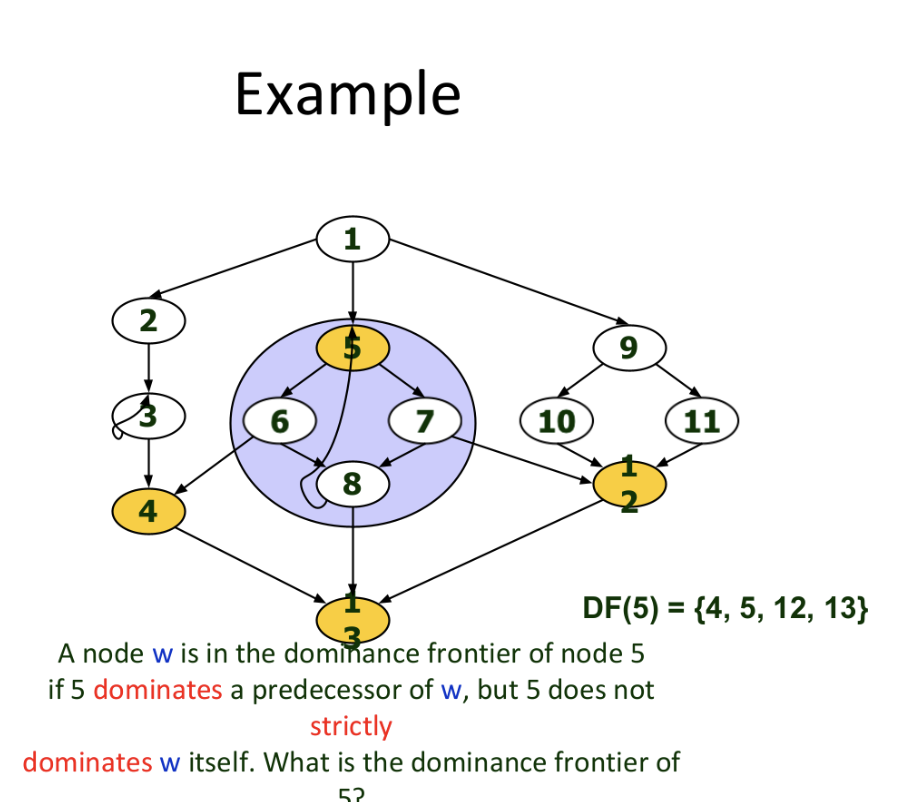
Correctness: so, the dominance frontier of $w$ is $\displaystyle\left(\bigcup_{v\in\text{dom}(w)}S(v)\right)\setminus\text{dom}(w)$, where $S$ is the successor function of $w$.
Note: $w$ only needs to dominate one predecessor of $w$.

We define the dominance frontier criterion for calculating phi function placement: if node $x$ contains a definition of variable $a$, then any node $z$ in the dominance frontier of $x$ needs a phi function for $a$.

Such a node needs to be a join node because it has a predecessor dominated by $x$, but also isn't dominated by $x$, implying a different predecessor that isn't dominated by $x$. So, two predecessors ⟹ join node.

The local dominance frontier $\text{DF}_\text{local}[n]$ of a node $n$ are the successors of $n$ in the CFG that aren't strictly dominated by $n$, i.e. are dominated by other nodes not through $n$. Again, this implies that any node in the local dominance frontier is a join node.

passed up?

The dominance frontier is inherited from children: $\text{DF}[n]$ consists of the local dominance frontier of $n$ and the the union of the

Compiler Design CMPUT415

V00 - Lexical Analysis and Parsing

Overview of Language Processing

Grammar Example: Generator Parser

V01 - Building an (LL1) Lexer and Parser from Scratch

Lexer from Scratch

Philosophy of the Lexer

Code

Parser from Scratch

Code

V02 - Language Hierarchy

Automata Theory Terms

Language Hierarchy

CSGs with ANTLR

V03 - Ambiguity

Ambiguity

WWAD: What Would ANTLR Do?

Different Ways to Illustrate a Grammar

V04 - LL and LR Recognizers

LL Parsers

LR Parsers

Characterizing Parsers

V05 - Parser Generators

Left-Recursion

Fixing the Problem

ANTLR and Left Recursion

V06 - Building a Recursive-Descent Recognizer from a Grammar

Program Structure

Rules and Tokens

Matching

Regex Constructs

Non-greedy Rules

V07 - Lookahead Sets and non-determinism

FIRST

FOLLOW and Empty Alternatives

Non-determinism

Left-factoring

V08 - LL(k) Recursive-Descent Parser Example

Program Structure

Parser Class

Lookahead Parser Class

Driver

Buffering the Token Stream

Non-LL(k) Grammars

Appendix: Why Doesn't Our Program Do Anything?

V09 - Listeners and Visitors

Discovery and Visit order

Walking the Parse Tree

Listeners and Visitors

Motivation

Visitor Pattern

Listener Pattern

WWAD

V0A - Decoupling Grammars from Application Code

Embedded Actions

Beginning to Decouple

Full Decoupling

Code

V0B - Handling Alternatives Ergonomically

Example

V0C - Sharing Information among Event Methods

Returning Values from visit

Stack Method

Parse-Tree Annotation (Listener or Visitor)

The Fourth Option: Retuning in the Grammar Directly

V0D - Visitor and Listener Examples from Scratch (Java)

V0E - Actions in Grammars

V0F - Semantic Predicates

Use-case

V10 - Lexical Modes and Island Grammars

V11 - Parsing DOT

Example DOT Program

Feature: Case-Independent Identifiers

Feature: Matching Angle Brackets

Naive Approaches

Solution

V12 - Symbols and Scopes

Symbols

Representing Symbols

Representing User-defined Types

Compiler Design `CMPUT415`

Returning Values from `visit`